Hostname: page-component-66644f4456-l2dlr Total loading time: 0 Render date: 2025-02-12T14:18:18.577Z Has data issue: true hasContentIssue false
  • English
  • Français

Topological Extension Properties and Projective Covers

Published online by Cambridge University Press:  20 November 2018

Haruto Ohta
Haruto Ohta*
Affiliation:
Shizuoka University, Ohya, Shizuoka, Japan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Introduction. All spaces considered in this paper are assumed to be (Hausdorff) completely regular, and all maps are continuous. Let 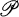be a topological property of spaces. We shall identify 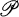with the class of spaces having 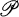. A space having 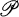is called a 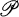-space, and a subspace of a 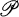-space is called a 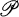-regular space. The class of 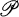-regular spaces is denoted by R(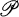). Following [37], we call a closed hereditary, productive, topological property 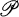such that each 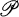-regular space has a 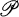-regular compactification a topological extension property, or simply, an extension property. In this paper, we restrict our attention to extension properties 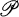satisfying the following axioms:

(A1) The two-point discrete space has .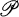

(A2) If each 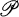-regular space of nonmeasurable cardinal has 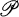, then 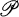= R().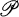

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 34 , Issue 6 , 01 December 1982 , pp. 1255 - 1275
Copyright
Copyright © Canadian Mathematical Society 1982

References

1. A. V, Arhangel'skiï, On a class of spaces containing all metric spaces and all locally bi-compact spaces, Amer. Math. Soc. Transi. (2) 92 (1970), 1–39.Google Scholar
2. Banaschewski, B., Uber nulldimensionale Raiime, Math. Nachr. 13 (1955), 129–140.Google Scholar
3. Broverman, S., Pseudocompactness properties, Proc. Amer. Math. Soc. 59 (1976), 175–178.Google Scholar
4. Broverman, S., N-compactness and weak homogeneity, Proc. Amer. Math. Soc. 62 (1977), 173–176.Google Scholar
5. Kim-Peu, Chew, A characterization of N-compact spaces, Proc. Amer. Math. Soc. 26 (1970), 679–682.Google Scholar
6. Comfort, W. W. and Negrepontis, S., Extending continuous functions on X X Y to subsets of pXXP Y, Fund. Math. 59 (1966), 1–12.Google Scholar
7. Dykes, N., Mappings and realcompact spaces, Pacific J. Math. 31 (1969), 347–358.Google Scholar
8. Engelking, R., General topology (Polish Scientific Publishers, Warszawa, 1977).Google Scholar
9. Engelking, R. and S, Mrôwka, On E-compact spaces, Bull. Acad. Polon. Sci. 6 (1958), 429–436.Google Scholar
10. Frolik, Z., A generalization of realcompact spaces, Czech. Math. J. 13 (1963), 123–137.Google Scholar
11. Gillman, L. and Jerison, M., Rings of continuous functions (Van Nostrand, Princeton, N.J., 1960).Google Scholar
12. Hardy, K. and Woods, R. G., On c-realcompact spaces and locally bounded normal functions, Pacific J. Math. 43 (1972), 647–656.Google Scholar
13. Herrlich, H., ℭ-kompakteRaiime, Math. Z. 96 (1967), 228–255.Google Scholar
14. Herrlich, H. and J, van der Slot, Properties which are closely related to compactness, Indag. Math. 29 (1967), 524–529.Google Scholar
15. Hong, S. S., On t-compactlike spaces and reflective subcategories, Gen. Top. Appl. 3 (1973), 319–330.Google Scholar
16. Husek, M., Perfect images of E-compact spaces, Bull. Acad. Polon. Sci. 20 (1972), 41–45.Google Scholar
17. Iliadis, S. and Fomin, S., The methods of centered systems in the theory of topological spaces, Russian Math. Surveys 21 (1966), 37–62.Google Scholar
18. Isiwata, T., Generalizations of M-spaces I, II, Proc. Japan Acad. Ser. A Math. Sci. 45 (1969), 359–363, 364-367.Google Scholar
19. Mack, J. E. and Johnson, D. G., The Dedekind completion of C(X), Pacific J. Math. 20 (1967), 231–243.Google Scholar
20. Michael, E. A., Bi-quotient maps and cartesian products of quotient maps, Ann. Inst. Fourier (Grenoble), 18 (1968), 287–302.Google Scholar
21. Michael, E. A., A quituple quotient quest, Gen. Top. Appl. 2 (1972), 91–138.Google Scholar
22. Morita, K., Products of normal spaces with metric spaces, Math. Ann. 154 (1964), 365–382.Google Scholar
23. Morita, K., Topological completions and M-spaces, Sci. Rep. Tokyo Kyoiku Daigaku, Sect. A 10 (1970), 271–288.Google Scholar
24. S, Mrôwka, On E-compact spaces II, Bull. Acad. Polon. Sci. 14 (1966), 597–605.Google Scholar
25. S, Mrôwka, Further results on E-compact spaces. I, Acta Math. 120 (1968), 161–185.Google Scholar
26. Ohta, H., On Hewitt realcompactifications of products, Ph.D. Thesis at the University of Tsukuba, (1979).Google Scholar
27. Ohta, H., Topologically complete spaces and perfect maps, Tsukuba J. Math. 1 (1977), 77–89.Google Scholar
28. Ohta, H., The Hewitt realcompactification of products, Trans. Amer. Math. Soc. 268 (1981), 363–375.Google Scholar
29. Przymusinski, T. C., Extending functions from products with a metric factor and absolutes, Pacific J. Math. 101 (1982), 463–475.Google Scholar
30. Siwiec, F., Sequence-covering and countably bi-quotient mappings, Gen. Top. Appl. 1 (1971), 143–154.Google Scholar
31. Siwiec, F. and Mancuso, V. J., Relations among certain mappings and conditions for their equivalence, Gen. Top. Appl. 1 (1971), 34–41.Google Scholar
32. Strauss, D., Extremally disconnected spaces, Proc. Amer. Math. Soc. 18 (1967), 305–309.Google Scholar
33. Terada, T., New topological extension properties, Proc. Amer. Math. Soc. 67 (1977), 162–166.Google Scholar
34. Woods, R. G., Co-absolutes of remainders of Stone-Cech compactifications, Pacific J. Math. 37 (1971), 545–560.Google Scholar
35. Woods, R. G., Ideals of pseudocompact regular closed sets and absolutes of Hewitt realcompactifications, Gen. Top. Appl. 2 (1972), 315–331.Google Scholar
36. Woods, R. G., A Tychonoff almost realcompactification, Proc. Amer. Math. Soc. 48 (1974), 200–208.Google Scholar
37. Woods, R. G., Topological extension properties, Trans. Amer. Math. Soc. 210 (1975), 365–385.Google Scholar
38. Woods, R. G., A survey of absolutes of topological spaces, Topological Structures II, Math. Centre Tracts 116 (1979), 323–362.Google Scholar