Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-24T11:27:38.195Z Has data issue: false hasContentIssue false
  • English
  • Français

A Theory of Uniformities for Generalized Ordered Spaces

Published online by Cambridge University Press:  20 November 2018

W. F. Lindgren  and
P. Fletcher
W. F. Lindgren
Affiliation:
Slippery Rock State College, Slippery Rock Pennsylvania
P. Fletcher
Affiliation:
Slippery Rock State College, Slippery Rock Pennsylvania
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let (X, 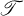) be a topological space equipped with a partial order ≦ and let C (≦) denote the continuous increasing functions mapping X into R (a function f : X → R is increasing provided f(x) ≦ f(y) whenever x ≦ y) Then (X,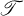, ≦) is an N-space (in the terminology of [16], a completely regular order space) provided 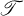is the weak topology of C (≦) and if x ≦ y is false, then there is an f ∈ C (≦) such that f(y) < f(x). L. Nachbin's introduction of N-spaces was perspicacious, for these spaces now find application in a wide spectrum of mathematics.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 31 , Issue 1 , 01 February 1979 , pp. 35 - 44
Copyright
Copyright © Canadian Mathematical Society 1979

References

1. Blatter, J., Order compactifications of totally ordered topological spaces, J. Approx. Theor. 13 (1975), 56–65.Google Scholar
2. Blatter, J. and Seever, G. L., Interposition and lattice cones of functions, Trans. Amer. Math Soc. 222 (1976), 65–96.Google Scholar
3. Cech, E., Topological spaces, Academia (Czechoslovak Acad. Sci.) Prague 1966.Google Scholar
4. Engelking, R. and Lutzer, D., Paracompactness in ordered spaces, Fund. Math. 94 (1977), 49–58.Google Scholar
5. Fletcher, P., Pairwise uniform spaces, Notices Amer. Math. Soc. 83 (1965), 612.Google Scholar
6. Gillman, L. and Henriksen, M., Concerning rings of continuous functions, Trans. Amer. Math. Soc. 77 (1954), 340–362.Google Scholar
7. Hajek, O., Absolute stability of noncompact sets, J. Differential Equation. 9 (1971), 496–508.Google Scholar
8. Hunsaker, W. and Lindgren, W. F., Construction of quasi-uniformities, Math. Ann. 188 (1970), 39–42.Google Scholar
9. Kaufman, R. P., Ordered sets and compact spaces. Colloq. Math. 17 (1967), 35–39.Google Scholar
10. Lawson, J. D., Intrinsic topologies in topological lattices and semilattices, Pacific J. Math. 44 (1973), 593–602.Google Scholar
11. Lindgren, W. F. and Fletcher, P., A construction of the pair completion of a quasi-uniform space, Can. Math. Bull., to appear.Google Scholar
12. Lutzer, D. J., On generalized ordered spaces, Dissertationes Math. Rozprawy Mat. 89 (1971).Google Scholar
13. Mansfield, M. J., Some generalizations of full normality, Trans. Amer. Math. Soc. 86 (1957), 489–505.Google Scholar
14. Mislove, M. W., Semigroups over trees, Trans. Amer. Math. Soc. 195 (1974), 383–400.Google Scholar
15. Murdeshwar, M. G. and Naimpally, S. A., Trennungsaxioms in quasi-uniform spaces, Nieuw Arch. Wisk. 14 (1966), 97–101.Google Scholar
16. Nachbin, L., Topology and order, Van Nostrand Mathematical Studies, No. 4 (Van Nostrand, N.Y., 1965).Google Scholar
17. Ng, Kung-Fu, On order and topological completeness, Math. Ann. 196 (1972), 171–176.Google Scholar
18. Peressini, A. L., Ordered topological vector spaces (Harper and Row N.Y., 1967).Google Scholar
19. Redfield, R. H., Uniformly convex totally ordered sets, Proc. Amer. Math. Soc. 51 (1975), 289–294.Google Scholar
20. Redfield, R. H., Ordering uniform completions of partially ordered sets, Can. J. Math. 26 (1974), 644–664.Google Scholar
21. Salbany, S., Bitopological spaces, compactifications and completions, Mathematical monographs of the University of Cape Town, No. 1. Cape Town (1974).Google Scholar
22. Thron, W. J. and Zimmerman, S. J., A characterization of order topologies by means of minimal Tropologies, Proc. Amer. Math. Soc. 27 (1971), 161–167.Google Scholar
23. Wong, Yau-chuen and Ng, Kung-Fu, Partially ordered topological vector spaces (Clarendon Press, Oxford, 1973).Google Scholar