Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Dulmage, A.L.
and
Mendelsohn, N.S.
1959.
A Note on the Stochastic Rank of a Bipartite Graph.
Canadian Mathematical Bulletin,
Vol. 2,
Issue. 3,
p.
159.
Mendelsohn, N. S.
and
Dulmage, A. L.
1959.
The Term and Stochastic Ranks of a Matrix.
Canadian Journal of Mathematics,
Vol. 11,
Issue. ,
p.
269.
Ryser, H. J.
1960.
Matrices of zeros and ones.
Bulletin of the American Mathematical Society,
Vol. 66,
Issue. 6,
p.
442.
Ryser, H. J.
1960.
Traces of Matrices of Zeros and Ones.
Canadian Journal of Mathematics,
Vol. 12,
Issue. ,
p.
463.
Fulkerson, D. R.
and
Ryser, H. J.
1961.
Widths and Heights of (0,1) -Matrices.
Canadian Journal of Mathematics,
Vol. 13,
Issue. ,
p.
239.
Fulkerson, D. R.
and
Ryser, H. J.
1962.
Multiplicities and Minimal Widths for (0, 1)-Matrices.
Canadian Journal of Mathematics,
Vol. 14,
Issue. ,
p.
498.
Dulmage, A. L.
and
Mendelsohn, N. S.
1962.
Matrices Associated With the Hitchcock Problem.
Journal of the ACM,
Vol. 9,
Issue. 4,
p.
409.
Dulmage, A. L.
and
Mendelsohn, N. S.
1963.
Two Algorithms for Bipartite Graphs.
Journal of the Society for Industrial and Applied Mathematics,
Vol. 11,
Issue. 1,
p.
183.
Haber, Robert M.
1963.
Minimal Term Rank of a Class of (0, 1)-Matrices.
Canadian Journal of Mathematics,
Vol. 15,
Issue. ,
p.
188.
Mesner, Dale M.
1964.
Traces of a Class Of (0, 1)-Matrices.
Canadian Journal of Mathematics,
Vol. 16,
Issue. ,
p.
82.
Fulkerson, D. R.
1964.
The Maximum Number of Disjoint Permutations Contained in a Matrix of Zeros and Ones.
Canadian Journal of Mathematics,
Vol. 16,
Issue. ,
p.
729.
Fenner, Trevor I.
and
Loizou, Georghios
1977.
Combinatorial aspects of rectangular non-negative matrices.
Discrete Mathematics,
Vol. 20,
Issue. ,
p.
217.
Brualdi, Richard A
1980.
Matrices of 0's and 1's with total support.
Journal of Combinatorial Theory, Series A,
Vol. 28,
Issue. 3,
p.
249.
Brualdi, Richard A.
1980.
Matrices of zeros and ones with fixed row and column sum vectors.
Linear Algebra and its Applications,
Vol. 33,
Issue. ,
p.
159.
Brualdi, Richard A.
and
Ross, Jeffrey A.
1980.
On Ryser's maximum term rank formula.
Linear Algebra and its Applications,
Vol. 29,
Issue. ,
p.
33.
Anstee, R.P
1985.
General forbidden configuration theorems.
Journal of Combinatorial Theory, Series A,
Vol. 40,
Issue. 1,
p.
108.
Michael, T.S.
1993.
The structure matrix of the class of r-multigraphs with a prescribed degree sequence.
Linear Algebra and its Applications,
Vol. 183,
Issue. ,
p.
155.
Kuba, Attila
and
Herman, Gabor T.
1999.
Discrete Tomography.
p.
3.
Tsurkov, Vladimir
and
Mironov, Anatoli
1999.
Minimax Under Transportation Constrains.
Vol. 27,
Issue. ,
p.
123.
Tsurkov, Vladimir
and
Mironov, Anatoli
1999.
Minimax Under Transportation Constrains.
Vol. 27,
Issue. ,
p.
169.
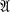 consisting of all (0, 1)-matrices of m rows and n columns, with row sum vector R and column sum vector S. Simple arithmetic properties of R and S are necessary and sufficient for the existence of a class
consisting of all (0, 1)-matrices of m rows and n columns, with row sum vector R and column sum vector S. Simple arithmetic properties of R and S are necessary and sufficient for the existence of a class 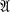 (1 ; 5).
(1 ; 5).

