Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-18T07:06:06.848Z Has data issue: false hasContentIssue false
  • English
  • Français

Systems of Weakly Coupled Hamilton-Jacobi Equations with Implicit Obstacles

Published online by Cambridge University Press:  20 November 2018

Diogo Gomes  and
António Serra
Diogo Gomes
Affiliation:
Departamento de Matemática, Instituto Superior Técnico, Universidade Técnica de Lisboa, Av. Rovisco Pais, 1049-001 Lisboa, Portugal email: [email protected], [email protected]
António Serra
Affiliation:
Departamento de Matemática, Instituto Superior Técnico, Universidade Técnica de Lisboa, Av. Rovisco Pais, 1049-001 Lisboa, Portugal email: [email protected], [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we study systems of weakly coupled Hamilton-Jacobi equations with implicit obstacles that arise in optimal switching problems. Inspired by methods from the theory of viscosity solutions and weak 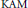$\text{KAM}$ theory, we extend the notion of Aubry set for these systems. This enables us to prove a new result on existence and uniqueness of solutions for the Dirichlet problem, answering a question of F. Camilli, P. Loreti, and N. Yamada.

Keywords

35F6035F2135D40Hamilton–Jacobi equationsswitching costsviscosity solutions
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 64 , Issue 6 , 01 December 2012 , pp. 1289 - 1309
Copyright
Copyright © Canadian Mathematical Society 2012

References

[1] Bardi, M. and I. Capuzzo-Dolcetta, Optimal control and viscosity solutions of Hamilton-Jacobi-Bellman equations. With appendices by Maurizio Falcone and Pierpaolo Soravia, Systems and Control: Foundations and Applications, Birkhäuser Boston Inc., Boston, MA, 1997.Google Scholar
[2] Barles, G., Solutions de viscosité des équations de Hamilton-Jacobi. Mathématiques & Applications (Berlin), 17, Springer-Verlag, Paris, 1994.Google Scholar
[3] Belbas, S. A., Optimal switching control of large scale energy generation systems: the method of quasi-variational inequalities. Rep. CSR 80-22. Electrical Enginnering Department, University of Maryland, College Park, 1980.Google Scholar
[4] Camilli, F., Loreti, P., and Yamada, N., Systems of convex Hamilton-Jacobi equations with implicit obstacles and the obstacle problem. Commun. Pure Appl. Anal. 8(2009), no. 4, 1291–1302. http://dx.doi.org/10.3934/cpaa.2009.8.1291 Google Scholar
[5] Capuzzo-Dolcetta, I. and Evans, L. C., Optimal switching for ordinary differential equations. SIAM J. Control Optim. 22(1984), no. 1, 143–161. http://dx.doi.org/10.1137/0322011 Google Scholar
[6] Capuzzo-Dolcetta, I., Matzeu, M., and Menaldi, J.-L., On a system of first-order quasivariational inequalities connected with the optimal switching problem. Systems Control Lett. 3(1983), no. 2, 113–116. http://dx.doi.org/10.1016/0167-6911(83)90009-9 Google Scholar
[7] Contreras, G., Action potential and weak KAM solutions. Calc. Var. Partial Differential Equations 13(2001), no. 4, 427–458. http://dx.doi.org/10.1007/s005260100081 Google Scholar
[8] Contreras, G., Iturriaga, R., Paternain, G. P., and Paternain, M., Lagrangian graphs, minimizing measures and Ma˜né's critical values. Geom. Funct. Anal. 8(1998), no. 5, 788–809. http://dx.doi.org/10.1007/s000390050074 Google Scholar
[9] Contreras, G., Delgado, J., and R. Iturriaga. Lagrangian flows: the dynamics of globally minimizing orbits. II. Bol. Soc. Brasil. Mat. (N. S.) 28(1997), no. 2, 155–196. http://dx.doi.org/10.1007/BF01233390 Google Scholar
[10] Crandall, M. G. and Lions, P.-L., Viscosity solutions of Hamilton-Jacobi equations. Trans. Amer. Math. Soc. 277(1983), no. 1, 1–42. http://dx.doi.org/10.1090/S0002-9947-1983-0690039-8 Google Scholar
[11] Dharmatti, S. and Ramaswamy, M., Hybrid control systems and viscosity solutions. SIAM J. Control Optim. 44(2005), no. 4, 1259–1288. http://dx.doi.org/10.1137/040618072 Google Scholar
[12] Engler, H. and Lenhart, S. M., Viscosity solutions for weakly coupled systems of Hamilton-Jacobi equations. Proc. London Math. Soc. (3) 63(1991), no. 1, 212–240. http://dx.doi.org/10.1112/plms/s3-63.1.212 Google Scholar
[13] Evans, L. C. and Friedman, A., Optimal stochastic switching and the Dirichlet problem for the Bellman equation. Trans. Amer. Math. Soc. 253(1979), 365–389. http://dx.doi.org/10.1090/S0002-9947-1979-0536953-4 Google Scholar
[14] Fathi, A., Weak KAM theorem and Lagrangian dynamics. Cambridge University Press, Cambridge, to appear.Google Scholar
[15] Fathi, A., Figalli, A., and Rifford, L., On the Hausdorff dimension of the Mather quotient. Comm. Pure Appl. Math. 62(2009), no. 4, 445–500. http://dx.doi.org/10.1002/cpa.20250 Google Scholar
[16] Fathi, A. and Maderna, E., Weak KAM theorem on non compact manifolds. No DEA Nonlinear Differential Equations Appl. 14(2007), no. 1-2, 1–27. http://dx.doi.org/10.1007/s00030-007-2047-6 Google Scholar
[17] Fathi, A. and Siconolfi, A., Existence of C1 critical subsolutions of the Hamilton-Jacobi equation. Invent. Math. 155(2004), no. 2, 363–388. http://dx.doi.org/10.1007/s00222-003-0323-6 Google Scholar
[18] Gomes, D., Viscosity solutions of Hamilton-Jacobi equations. Publicaç˜oes Matemáticas do IMPA. [IMPA Mathematical Publications]. 27-th Brazilian Mathematics Colloquium, Instituto Nacional de Matemática Pura e Aplicada (IMPA), Rio de Janeiro, 2009,Google Scholar
[19] Ishii, H., Perron's method for Hamilton-Jacobi equations. Duke Math. J. 55(1987), no. 2, 369–384. http://dx.doi.org/10.1215/S0012-7094-87-05521-9 Google Scholar
[20] Ishii, H., Asymptotic solutions for large time of Hamilton-Jacobi equations in Euclidean n space. Ann. Inst. H. Poincaré Anal. Non Linéaire 25(2008), no. 2, 231–266. http://dx.doi.org/10.1016/j.anihpc.2006.09.002 Google Scholar
[21] Ishii, H. and Mitake, H., Representation formulas for solutions of Hamilton-Jacobi equations with convex Hamiltonians. Indiana Univ. Math. J. 56(2007), no. 5, 2159–2183. http://dx.doi.org/10.1512/iumj.2007.56.3048 Google Scholar
[22] Lenhart, S. M. and Belbas, S. A., A system of nonlinear partial differential equations arising in the optimal control of stochastic systems with switching costs. SIAM J. Appl. Math. 43(1983), no. 3, 465–475. http://dx.doi.org/10.1137/0143030 Google Scholar
[23] Lions, P.-L., Generalized solutions of Hamilton-Jacobi equations. Research Notes in Mathematics, 69, Pitman (Advanced Publishing Program), Boston, Mass.-London, 1982.Google Scholar
[24] Ma˜né, R., Lagrangian flows: the dynamics of globally minimizing orbits. In: International Conference on Dynamical Systems (Montevideo, 1995), Pitman Res. Notes Math. Ser., 362, Longman, Harlow, 1996, pp. 120–131.Google Scholar
[25] Ma˜né, R., Lagrangian flows: the dynamics of globally minimizing orbits. Bol. Soc. Brasil. Mat. (N. S.) 28(1997), no. 2, 141–153. http://dx.doi.org/10.1007/BF01233389 Google Scholar
[26] Mather, J. N., Total disconnectedness of the quotient Aubry set in low dimensions. Comm. Pure Appl. Math. 56(2003), no. 8, 1178–1183. http://dx.doi.org/10.1002/cpa.10091 Google Scholar
[27] Mather, J. N., Examples of Aubry sets. Ergodic Theory Dynam. Systems 24(2004), no. 5, 1667–1723. http://dx.doi.org/10.1017/S0143385704000446 Google Scholar
[28] Sorrentino, A., On the total disconnectedness of the quotient Aubry set. Ergodic Theory Dynam. Systems 28(2008), no. 1, 267–290.Google Scholar
[29] Zhang, H. and James, M. R., Optimal control of hybrid systems and a system of quasi-variational inequalities. SIAM J. Control Optim. 45(2006), no. 2, 722–761. http://dx.doi.org/10.1137/050630131Google Scholar