Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-12-02T23:32:16.615Z Has data issue: false hasContentIssue false
  • English
  • Français

Synthese Harmonique Des Sous-Groupes Discrets

Published online by Cambridge University Press:  20 November 2018

N. Lohoué
N. Lohoué*
Affiliation:
Université Par is-Sud, Centre d'Orsay 91-ORSAY (France)
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Dans [4] C. S. Herz soulève la question suivante:

Soit G = SL(2, R) le groupe des matrices réelles d'order deux, de déterminant un; soit H = SL(2, Z) le sous-groupe discret de G, formé des matrices à coefficients entiers. Existe-t-il une constante absolue c > 0 telle que pour toute function f de At(H) à support fini, on puisse trouver une function 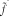de AP(G), à support compact dont la restriction à H coïncide a vec f et

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 27 , Issue 4 , 01 August 1975 , pp. 792 - 796
Copyright
Copyright © Canadian Mathematical Society 1975

References

Bibliographie

1. Eymard, P., Algèbres Ap et convoluteurs de LP(G), Sém. N. Bourbaki, 22ème année, exposé 367, Paris.Google Scholar
2. Dieudonne, J., Sur le produit de composition, II, J. Math. Pures Appl. 39 (1960), 275–292.Google Scholar
3. Dixmier, J., Les algèbres d'opérateurs dans l'espace hilbertien, 2ème éd (Gauthier-Villars, Paris, 1969).Google Scholar
4. Herz, C. S., Conference on harmonie analysis, Maryland, Lecture Notes 226 (Springer-Verlag, 1972).Google Scholar
5. Kunze, R. A. and Stein, E. M., Uniformly bounded representations and harmonic of 2 real unimodular groups, I. A. J. Maths. 82 (1960), 1–62.Google Scholar
6. Takesaki, M. and Tatsuuma, N., Duality and subgroups, II, J. Functional Analysis 11 (1972), 184–185.Google Scholar