Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-27T23:04:20.174Z Has data issue: false hasContentIssue false
  • English
  • Français

Symmetrizable, 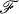-, and Weakly First Countable Spaces

Published online by Cambridge University Press:  20 November 2018

R. M. Stephenson
R. M. Stephenson*
Affiliation:
University of South Carolina, Columbia, South Carolina
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A number of results are given concerning the character and cardinality of symmetrizable and related spaces. An example is given of a symmetrizable Hausdorff space containing a point that is not a regular Gδ , and a proof is given that if a point p of a symmetrizable Hausdorff space has a neighborhood base of cardinality 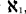, then p is a Gδ . It is shown that for each cardinal number m there exists a locally compact, pseudocompact, Hausdorff 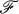-space X with |X| ≧ m. Several questions of A. V. Arhangel'skii and E. Michael are partially answered.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 29 , Issue 3 , 01 June 1977 , pp. 480 - 488
Copyright
Copyright © Canadian Mathematical Society 1977

References

1. Arhangel'skii, A. V., Mappings and spaces, Uspehi Mat. Nauk 21 (1966), no. 4 ﹛130), 133-184 Russian Math. Surveys 21 (1966), no. 4, 115–162.Google Scholar
2. Arhangel'skii, A. V. On the cardinality of bicompacta satisfying the first axiom of countability, Soviet Math. Dokl 10 (1969), 951–955.Google Scholar
3. Bonnett, D. A., A symmetrizable space that is not perfect, Proc. Amer. Math. Soc. 34 (1972), 560–564.Google Scholar
4. Franklin, S. P., Spaces in which sequences suffice, II, Fund. Math. 57 (1967), 51–56.Google Scholar
5. Gillman, L. and Jerison, M., Rings of continuous functions (Van Nostrand, Princeton, N.J., 1960).Google Scholar
6. Harley, Peter W., III and Stephenson, R. M., Jr., Symmetrizable and related spaces, Trans. Amer. Math. Soc. 217 (1976), to appear.Google Scholar
7. Nedev, S., Symmetrizable spaces and final compactness, Soviet Math. Dokl. 8 (1967), 890–892.Google Scholar