Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-25T05:52:58.939Z Has data issue: false hasContentIssue false
  • English
  • Français

Symmetric Exterior Differentiation and Flat Forms

Published online by Cambridge University Press:  20 November 2018

Victor L. Shapiro
Victor L. Shapiro*
Affiliation:
University of Oregon
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let ω be a continuous differential r-form defined in a bounded domain R of Euclidean n-space, En, where n ≧ 1 and 0 ≦ r ≦ n — 1. ω is called a flat form in R, (3, p. 263), if there exists a constant N such that 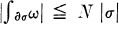for every (r + 1)-simplex σ contained in R, where |σ| designates the (r + 1)-volume of σ. For n = 1 and ω a zero form, flatness is the same thing as the usual Lip 1 condition. As is well known, a necessary and sufficient condition that a continuous real-valued function of one variable f(x) satisfy a Lip 1 condition over an interval (a, b) is that its upper and lower symmetric derivatives be bounded in (a, b) (4, pp. 22, 327). We intend to prove the analogue of this result for r-forms.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 14 , 1962 , pp. 79 - 86
Copyright
Copyright © Canadian Mathematical Society 1962

References

1. Bochner, S., Summation of multiple Fourier series by spherical means, Trans. Amer. Math. Soc., 40 (1936), 175–207.Google Scholar
2. Shapiro, V. L., The divergence theorem for discontinuous vector fields, Ann. Math., 68 (1958), 604–624.Google Scholar
3. Whitney, H., Geometric integration theory (Princeton, 1957).Google Scholar
4. Zygmund, A., Trigonometric series (Cambridge, 1959), I. Google Scholar