Article contents
Sur L'Approximation Polynomiale Sur Tout L'axe Reel
Published online by Cambridge University Press: 20 November 2018
Extract
Soit Q(x) une fonction positive paire continûment différentiable pour — ∞ < x < ∞ telle que xQ’ (x) soit croissante pour x > 0 et que Q‘(x) → ∞ lorsque x → co. Désignons par Qn l'unique racine positive de l'équation xQ‘(x) = n. L'approximation polynomiale des fonctions continues relativement au poids e-Q(x) a été étudiée par de nombreux mathématiciens. Le résultat suivant est une conséquence d'un théorème de l'un des auteurs (voir Freud [1]): si F(x) est une fonction réelle continue pour —∞ < x < ∞ qui satisfait une condition de Lipschitz d'ordre a où 0 < a < 1, il existe une suite de polynômes ﹛Pn(x)﹜ où deg Pn ≦ n telle que
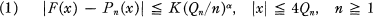
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1976
References
Bibliographie
- 2
- Cited by


