Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Mazorchuk, Volodymyr
and
Stroppel, Catharina
2008.
Categorification of (induced) cell modules and the rough structure of generalised Verma modules.
Advances in Mathematics,
Vol. 219,
Issue. 4,
p.
1363.
Mazorchuk, Volodymyr
2010.
Classification of simple $\mathfrak{q}_2$-supermodules.
Tohoku Mathematical Journal,
Vol. 62,
Issue. 3,
Kåhrström, Johan
and
Mazorchuk, Volodymyr
2010.
A new approach to Kostant’s problem.
Algebra & Number Theory,
Vol. 4,
Issue. 3,
p.
231.
KÅHRSTRÖM, JOHAN
2010.
KOSTANT'S PROBLEM AND PARABOLIC SUBGROUPS.
Glasgow Mathematical Journal,
Vol. 52,
Issue. 1,
p.
19.
Guo, Xiangqian
and
Liu, Xuewen
2011.
Whittaker modules over Virasoro-like algebra.
Journal of Mathematical Physics,
Vol. 52,
Issue. 9,
Batra, Punita
and
Mazorchuk, Volodymyr
2011.
Blocks and modules for Whittaker pairs.
Journal of Pure and Applied Algebra,
Vol. 215,
Issue. 7,
p.
1552.
Guo, Xiangqian
and
Liu, Xuewen
2011.
Whittaker Modules over Generalized Virasoro Algebras.
Communications in Algebra,
Vol. 39,
Issue. 9,
p.
3222.
Liu, Xuewen
and
Guo, Xiangqian
2013.
Whittaker modules over loop Virasoro algebra.
Frontiers of Mathematics in China,
Vol. 8,
Issue. 2,
p.
393.
Cai, Yan-an
Liu, Genqiang
Nilsson, Jonathan
and
Zhao, Kaiming
2018.
Generalized Verma modules over sln+2 induced from U(hn)-free sln+1-modules.
Journal of Algebra,
Vol. 502,
Issue. ,
p.
146.
Li, Yi-Yang
Shu, Bin
and
Yao, Yu-Feng
2020.
A criterion for irreducibility of parabolic baby Verma modules of reductive Lie algebras.
Journal of Algebra,
Vol. 563,
Issue. ,
p.
111.
Chen, Chih-Whi
2021.
Whittaker Modules for Classical Lie Superalgebras.
Communications in Mathematical Physics,
Vol. 388,
Issue. 1,
p.
351.
Chen, Chih-Whi
Coulembier, Kevin
and
Mazorchuk, Volodymyr
2021.
Translated simple modules for Lie algebras and simple supermodules for Lie superalgebras.
Mathematische Zeitschrift,
Vol. 297,
Issue. 1-2,
p.
255.
Bai, Zhanqiang
and
Xiao, Wei
2021.
Reducibility of generalized Verma modules for Hermitian symmetric pairs.
Journal of Pure and Applied Algebra,
Vol. 225,
Issue. 4,
p.
106561.
Xiao, Wei
and
Zhang, Ailin
2022.
Jantzen coefficients and simplicity of parabolic Verma modules.
Journal of Algebra,
Vol. 611,
Issue. ,
p.
24.
Mackaay, Marco
Mazorchuk, Volodymyr
and
Miemietz, Vanessa
2024.
Applying projective functors to arbitrary holonomic simple modules.
Journal of the London Mathematical Society,
Vol. 110,
Issue. 2,
Chen, Chih-Whi
2024.
Kostant’s problem for Whittaker modules.
Letters in Mathematical Physics,
Vol. 114,
Issue. 1,
Mazorchuk, Volodymyr
and
Srivastava, Shraddha
2025.
Kostant’s problem for parabolic Verma modules.
Proceedings of the Edinburgh Mathematical Society,
p.
1.
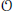 $\mathcal{O}$
and prove that the blocks of this parabolic category are equivalent to certain blocks of the category of Harish-Chandra bimodules. From this we derive, in particular, an irreducibility criterion for generalized Verma modules. We also compute the composition multiplicities of those simple subquotients, which correspond to the induction from simple modules whose annihilators are minimal primitive ideals.
$\mathcal{O}$
and prove that the blocks of this parabolic category are equivalent to certain blocks of the category of Harish-Chandra bimodules. From this we derive, in particular, an irreducibility criterion for generalized Verma modules. We also compute the composition multiplicities of those simple subquotients, which correspond to the induction from simple modules whose annihilators are minimal primitive ideals.

