Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Medini, Andrea
2011.
Products and h-homogeneity.
Topology and its Applications,
Vol. 158,
Issue. 18,
p.
2520.


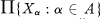 admit continuous extensions to
admit continuous extensions to 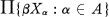 where
where  have clopen closures in
have clopen closures in 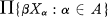 .
.