Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T06:03:04.934Z Has data issue: false hasContentIssue false
  • English
  • Français

Strongly Incompressible Curves

Published online by Cambridge University Press:  20 November 2018

Mario Garcia-Armas
Mario Garcia-Armas*
Affiliation:
Department of Mathematics, University of British Columbia, Vancouver, BC V6T 1Z2, Canada e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

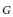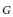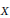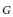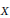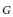Let $G$ be a finite group. A faithful $G$ -variety $X$ is called strongly incompressible if every dominant $G$ -equivariant rationalmap of $X$ onto another faithful $G$ -variety 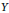$Y$ is birational. We settle the problem of existence of strongly incompressible 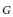$G$ -curves for any finite group 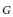$G$ and any base field 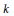$k$ of characteristic zero.

Keywords

14L3014E0714H37algebraic curvesgroup actionsGalois cohomology
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 68 , Issue 3 , 01 June 2016 , pp. 541 - 570
Copyright
Copyright © Canadian Mathematical Society 2016

References

[BeaulO] Beauville, A., Finite subgroups of PGL2(K), Vector bundles and complex geometry 23–29, Contemp. Math., 522, Amer. Math. Soc, Providence, RI, 2010.Google Scholar
[BF03] Berhuy, G. and Favi, G., Essential dimension: functorial point of view (after A. Merkurjev). Doc. Math. 8 (2003), 279–330.Google Scholar
[ChlO] Chen, X., Self rational maps ofK3 surfaces, 2010, arXiv:1008.1619vl [math.AG].Google Scholar
[Chl2] Chen, X., Rational self maps ofCalabi-Yau manifolds. To appear. (Available online at http://www.math.ualberta.ca/xichen/paper/cyself.pdf) Google Scholar
[EW87] Elman, R. and Wadsworth, A. R., Hereditarily quadratically closed fields. J. Algebra 111(1987), no. 2, 475–482.http://dx.doi.org/10.101 6/0021-8693(87)90231-6 Google Scholar
[EK94] Epkenhans, M. and Kriiskemper, M., On trace forms of étale algebras and field extensions. Math. Z. 217(1994), no. 3, 421–434. http://dx.doi.org/10.1007/BF02571952 Google Scholar
[FJ08] Fried, M. D. and Jarden, M., Field arithmetic. Third edition. Ergebnisse der Mathematik und ihrer Grenzgebiete, 3. Folge, A Series of Modern Surveys in Mathematics, 11, Springer-Verlag,Berlin, 2008.Google Scholar
[Gal3] Garcia-Armas, M., Finite group actions on curves of genus zero. J. Algebra 394(2012), 173–181.http://dx.doi.Org/10.1016/j.jalgebra.2013.07.018 Google Scholar
[LamO5] Lam, T. Y., Introduction to quadratic forms over fields. Graduate Studies in Mathematics 67,American Mathematical Society, Providence, RI, 2005.Google Scholar
[LT58] Lang, S. and Tate, J., Principal homogeneous spaces over abelian varieties.Amer. J. Math. 80(1958),659–684.http://dx.doi.org/10.2307/2372778 Google Scholar
[LeO7] Ledet, A., Finite groups of essential dimension one. J. Algebra 311(2007), no. 1, 31–37.http://dx.doi.Org/10.1016/j.jalgebra.2006.12.027 Google Scholar
[LiuO2] Liu, Q., Algebraic geometry and arithmetic curves. Oxford Graduate Texts in Mathematics 6, Oxford University Press, Oxford, 2002.Google Scholar
[Me91] Mestre, J.-F, Construction de courbes de genre 2 á partir de leurs modules. Effective methods in algebraic geometry (Castiglioncello, 1990), 313–334, Progr. Math. 94, Birkhä user Boston, Boston, MA, 1991.Google Scholar
[ReOO] Reichstein, Z., On the notion of essential dimension for algebraic groups. Transform. Groups 5(2000), no. 3, 265–304.http://dx.doi.Org/1 0.1007/BF01 679716 Google Scholar
[Re04] Reichstein, Z., Compressions of group actions. Invariant theory in all characteristics, 199–202, CRM Proc. Lecture Notes, 35, Amer. Math. Soc, Providence, RI, 2004.Google Scholar
[RelO] Reichstein, Z. , Essential dimension. Proceedings of the International Congress of Mathematicians 2010 (ICM 2010), 162–188.Google Scholar
[RY01] Reichstein, Z. and Youssin, B., Splitting fields ofG-varieties. Pacific J. Math. 200(2001), no. 1,207Â249.http://dx.doi.org/10.2140/pjm.2001.200.207 Google Scholar
[Ros56] Rosenlicht, M., Some basic theorems on algebraic groups. Amer. J. Math. 78(1956), 401–443.http://dx.doi.org/10.2307/2372523 Google Scholar
[Ros63] Rosenlicht, M., A remark on quotient spaces. An. Acad. Brasil. Ci. 35(1963), 487–489.Google Scholar
[Se84] Serre, J.-P., L'invariant de Witt de la forme Tr(2). Comment. Math. Helv. 59(1984), no. 4, 651–676.Google Scholar
[SeO2] Serre, J.-P., Galois cohomology, Springer Monographs in Mathematics, Springer-Verlag, Berlin, 2002.Google Scholar
[SeO3] Serre, J.-P., Cohomological invariants, Witt invariants, and trace forms. Notes by Skip Garibaldi. Univ. Lecture Ser., 28, Cohomological invariants in Galois cohomology, 1–100, Amer. Math. Soc, Providence, RI, 2003.Google Scholar
[SeO8] Serre, J.-P., Topics in Galois theory. Second edition, With notes by Henri Darmon, Research Notes in Mathematics 1. A K Peters, Ltd., Wellesley, MA, 2008.Google Scholar
[ShO3] Shaska, T., Determining the automorphism group of a hyperelliptic curve. Proceedings of the 2003 International Symposium on Symbolic and Algebraic Computation, ACM, New York, 2003, pp. 248–254 (electronic).Google Scholar
[SilO9] Silverman, J. H., The arithmetic of elliptic curves. Second edition, Graduate Texts in Mathematics 106. Springer, Dordrecht, 2009.Google Scholar
[Vi88] Vila, N., On stem extensions ofSn as Galois group over number fields. J. Algebra 116(1988), no. 1, 251–260. http://dx.doi.Org/10.1 01 6/0021-8693(88)90205-0 Google Scholar