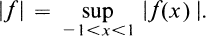No CrossRef data available.
Published online by Cambridge University Press: 20 November 2018
We denote by E the open unit disc in C and by H(E) the class of all analytic functions f on E with f(0) = 0. Let (see [3] for more complete definitions)
S = {ƒ ∈ H(E)|ƒ is univalent on E}
S0 = {ƒ ∈ H(E)|ƒ is starlike univalent on E}
TR = {ƒ ∈ H(E)|ƒ is typically real on E}.
The uniform norm on (— 1, 1) of a function ƒ ∈ H(E) is defined by