Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-28T05:52:29.892Z Has data issue: false hasContentIssue false
  • English
  • Français

Stark's Conjecture and New Stickelberger Phenomena

Published online by Cambridge University Press:  20 November 2018

Victor P. Snaith
Victor P. Snaith*
Affiliation:
Department of Pure Mathematics, University of Sheffield, Sheffield S3 7RH, U.K. e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We introduce a new conjecture concerning the construction of elements in the annihilator ideal associated to a Galois action on the higher-dimensional algebraic 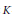$K$-groups of rings of integers in number fields. Our conjecture ismotivic in the sense that it involves the (transcendental) Borel regulator as well as being related to 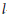$l$–adic étale cohomology. In addition, the conjecture generalises the wellknown Coates–Sinnott conjecture. For example, for a totally real extension when 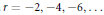$r\,=\,-2,\,-4,\,-6,\,\ldots $ the Coates–Sinnott conjecture merely predicts that zero annihilates 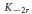${{K}_{-2r}}$ of the ring of 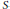$S$–integers while our conjecture predicts a non-trivial annihilator. By way of supporting evidence, we prove the corresponding (conjecturally equivalent) conjecture for the Galois action on the étale cohomology of the cyclotomic extensions of the rationals.

Keywords

11G5511R3411R4219F27
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 58 , Issue 2 , 01 April 2006 , pp. 419 - 448
Copyright
Copyright © Canadian Mathematical Society 2006

References

[1] Banaszak, G., Algebraic K-theory of number fields and rings of integers and the Stickelberger ideal. Annals of Math. 135(1992), no. 2, 325–360.Google Scholar
[2] Benois, D. and Nguyen Quang Do, T., Les nombres de Tamagawa locaux et la conjecture de Bloch et Kato pour les motifs ℚ(m . sur un corps abélien. Ann. Sci. éc. Norm. Sup. 35(2002), 641–672.Google Scholar
[3] Beilinson, A., Polylogarithms and cyclotomic elements. preprint (1990).Google Scholar
[4] Brumer, A., On the units of algebraic number fields. Mathematika 14(1967), 121–124.Google Scholar
[5] Burgos, J. I. The regulators of Beilinson and Borel. CRM Monograph 15, American Mathematical Society, Providence, RI, 2002.Google Scholar
[6] Burns, D. and Greither, C., On the equivariant Tamagawa number conjecture for Tate motives. Invent. Math. 153(2003), no. 2, 303–359.Google Scholar
[7] Burns, D. and Greither, C., Equivariant Weierstrass preparation and values of L-functions at negative integers. Doc. Math. (2003) Extra volume in honour of Kazuya Kato, pp. 157–185.Google Scholar
[8] Cassou-Noguès, P., Valeurs aux entiers négatifs des fonctions zêta et fonctions zêta p-adiques. Invent. Math. 51(1979), 29–59.Google Scholar
[9] Coates, J. H. p-adic L-functions and Iwasawa theory. In: Algebraic Number Fields, L-Functions and Galois Properties, Academic Press, London, 1977, pp. 269–353.Google Scholar
[10] Coates, J. H. and Sinnott, W., An analogue of Stickelberger's theorem for the higher K-groups. Invent. Math. 24(1974), 149–161.Google Scholar
[11] Coates, J. H. and Sinnott, W., On p-adic L-functions over real quadratic fields. InventMath. 25(1974), 253–279.Google Scholar
[12] Cornacchia, P. and Greither, C., Fittings ideals of class-groups of real fields with prime power conductor. J. Number Theory 73(1998), no. 2, 459–471.Google Scholar
[13] Cornacchia, P. and Ostvaer, P. A. On the Coates–Sinnott conjecture. K-Theory 19(2000), no. 2, 195–209.Google Scholar
[14] Curtis, C. W. and Reiner, I., Methods of Representation Theory. vols. I & II, Wiley (1981,1987).Google Scholar
[15] Dwyer, W. G. and Friedlander, E. M. Algebraic and étale K-theory. Trans. Amer. Math. Soc. 292(1985), no. 1, 247–280.Google Scholar
[16] Dwyer, W., Friedlander, E. M. V. Snaith, P. and R.Thomason, W., Algebraic K-theory eventually surjects onto topological K-theory. Invent.Math. 66(1982), no. 3, 481–491.Google Scholar
[17] Deligne, P. and Ribet, K., Values of abelian L-functions at negative integers over totally real fields. Invent.Math. 59(1980), no. 3, 227–286.Google Scholar
[18] Eisenbud, D., Commutative Algebra. With a view toward algebraic geometry. Graduate Texts in Mathematics 150, Springer-Verlag, New York, 1995.Google Scholar
[19] Geisser, T. and Levine, M., The Bloch-Kato conjecture and a theorem of Suslin-Voevodsky. J. Reine. Angew. Math. 530(2001), 55–103.Google Scholar
[20] Grayson, D., Higher algebr aic K-theory II (after D.G. Quillen). In: Algebraic K-theory, Lecture Notes in Math. 551, Springer Verlag. Berlin. 1976, pp. 217–240,Google Scholar
[21] Greither, C., Some cases of Brumer's conjecture for abelian CM extensions of totally real fields. Math. Z. 233(2000), no. 3, 515–534.Google Scholar
[22] Gross, B. H. On the values of Artin L-functions. Unpublished preprint, 1981. http://abel.math.harvard.edu/∼gross/preprints/ Google Scholar
[23] Hayes, D. R. Base change for the conjecture of Brumer-Stark. J. Reine. Angew.Math. 497(1998), 83–89.Google Scholar
[24] Huber, A. and Wildeshaus, J., Classical motivic polylogarithm according to Beilinson and Deligne. Doc. Math. 3(1998) 27–133 (electronic).Google Scholar
[25] Kolster, M., Nguyen Quang Do, T. and Fleckinger, V., Twisted S-units, p-adic class number formulas and the Lichtenbaum conjectures. Duke J. Math. 84(1996), 679–717 (erratum Duke J. Math. 90 (1997) 641-643 plus further corrigenda in [2] and [26]).Google Scholar
[26] Kolster, M., Nguyen Quang Do, T., Universal distribution lattices for abelian number fields. McMaster University preprint (2000).Google Scholar
[27] Kubota, T. and Leopoldt, H., Eine p-adische Theorie der Zetawerte. J. Reine. Angew. Math. 214/215(1964), 328–339.Google Scholar
[28] Kurihara, M., Iwasawa theory and Fitting ideals. J. Reine. Angew.Math. 561(2003), 39–86.Google Scholar
[29] Lang, S., Algebra. Second ed. Addison-Wesley, Reading, MA, 1984.Google Scholar
[30] Le Floc’h, M., On fitting ideals of certain étale K-groups. K-Theory 27(2002), 281–292.Google Scholar
[31] Levine, M., The indecomposable K3 of a field. Ann. Sci. école Norm. Sup. 22(1989), 255–344.Google Scholar
[32] Levine, M., Relative Milnor K-theory. K-Theory 6(1992), no. 2, 113–175. (Corrigendum: K-Theory 9(1995), no. 5, 503–505).Google Scholar
[33] Lichtenbaum, S., Values of zeta functions, étale cohomology and algebraic K-theory. In: Algebraic K-theory. II, Lecture Notes in Math. 342, Springer, Berlin, 1973, pp. 489–501.Google Scholar
[34] Martinet, J., Character theory and Artin L-functions. In: Algebraic Number Fields, Academic Press, London, 1977, pp. 1–87.Google Scholar
[35] Mazur, B. and Wiles, A., Class fields of abelian extensions of ℚ. Invent. Math. 76(1984), 179–330.Google Scholar
[36] Merkurjev, A. S. and Suslin, A. A. The K3 group for a field. Izv. Akad. Nauk. SSSR 54(1990), 339–356 (Eng. trans. Math. USSR-Izv. 36(1990), 541–565).Google Scholar
[37] Nguyen Quang Do, T., Conjecture Principale équivariante, idéaux de Fitting et annulateurs en théorie d’Iwasawa. to appear J. Théorie de Nombres de Bordeaux (special issue dedicated to G. Gras).Google Scholar
[38] Neukirch, J., The Beilinson conjecture for algebraic number fields. In: Beilinson's Conjectures on Special Values of L-Functions. Perspect. Math. 4, Academic Press, Boston, MA, 1988, pp. 193–247.Google Scholar
[39] Northcott, D. G., Finite Free Resolutions. Cambridge Tracts in Mathematics 71, Cambridge, Cambridge University Press, 1976.Google Scholar
[40] Queyrut, J., S-groupes des classes d’un ordre arithmétique. J. Algebra 76(1982), no. 1, 234–260.Google Scholar
[41] Quillen, D. G. Higher algebraic K-theory. I. In: Algebraic K-Theory. I, Lecture Notes in Math. 341, Springer, Berlin, 1973, pp. 85–147.Google Scholar
[42] Rognes, J. and Weibel, C. A., Two-primary algebraic K-theory of rings of integers in number fields. J. Amer.Math. Soc. 13(2000), no. 1, 1–54.Google Scholar
[43] Sands, J., Abelian fields and the Brumer-Stark conjecture. Compositio Math. 53(1984), no. 3, 337–346.Google Scholar
[44] Sands, J., Base change for higher Stickelberger ideals. J. Number Theory 73(1998), no. 2, 518–526.Google Scholar
[45] Serre, J-P., Linear Representations of Finite Groups. Graduate Texts in Mathematics 42, Springer-Verlag, New York, 1977.Google Scholar
[46] Siegel, C., Uber die Fouriersche Koeffizienten von Modulformen. Nachr. Akad. Wiss. Göttingen Math.-Phys. Kl. II 3, (1970), 1–56.Google Scholar
[47] Snaith, V. P., Algebraic K-groups as GaloisModules. Progress in Mathematics 206, Birkhäuser Verlag, Basel, 2002.Google Scholar
[48] Snaith, V. P., Equivariant motivic phenomena. In: Axiomatic, enriched and motivic homotopy theory, NATO Sci. Series II 131, Kluwer, Dordrecht, 2004, pp. 335–383.Google Scholar
[49] Snaith, V. P., Relative K 0, annihilators, Fitting ideals and the Stickelberger phenomena. Proc. London Math. Soc. 90(2005), no. 3, 545–590.Google Scholar
[50] Stickelberger, L., Über eine Verallgemeinerung der Kreistheilung. Math. Annalen 37(1890), 321–367.Google Scholar
[51] Swan, R. G. Algebraic K-theory. Lecture Notes in Math. 76 Springer-Verlag, Berlin, 1968.Google Scholar
[52] Tate, J. T., Relations between K. and Galois cohomology. Invent.Math. 36(1976), 257–274.Google Scholar
[53] Tate, J. T., Les Conjectures de Stark sur les fonctions L d’Artin en s = 0. Progress in Mathematics 47, Birkhäuser, Boston, 1984.Google Scholar
[54] Voevodsky, V., The Milnor conjecture. http://www.math.uiuc.edu/K-theory. Google Scholar
[55] Voevodsky, V., On 2-torsion in motivic cohomology. http://www.math.uiuc.edu/K-theory. Google Scholar
[56] Voevodsky, V., On motivic cohomology with Z/l coefficients. http://www.math.uiuc.edu/K-theory. Google Scholar
[57] Washington, L., Introduction to Cyclotomic Fields. Second edition. Graduate Texts in Mathematics 83, Springer-Verlag, New York, 1997.Google Scholar
[58] Wiles, A., The Iwasawa conjecture for totally real fields. Ann. of Math. 131(1990), no. 3, 493–540.Google Scholar
[59] Wiles, A., On a conjecture of Brumer. Ann. of Math. 131(1990), no. 3, 555–565.Google Scholar