Stable Discrete Series Characters at Singular Elements

Abstract

Write 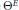${{\Theta }^{E}}$ for the stable discrete series character associated with an irreducible finite-dimensional representation 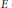$E$ of a connected real reductive group $G$. Let 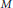$M$ be the centralizer of the split component of a maximal torus 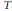$T$, and denote by 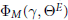${{\Phi }_{M}}\left( \gamma ,\,{{\Theta }^{E}} \right)$ Arthur’s extension of 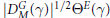$|D_{M}^{G}\,\left( \gamma \right)|{{\,}^{1/2}}\,{{\Theta }^{E}}\,\left( \gamma \right)$ to 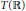$T\left( \mathbb{R} \right)$. In this paper we give a simple explicit expression for 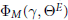${{\Phi }_{M}}\left( \gamma ,\,{{\Theta }^{E}} \right)$ when $\gamma $ is elliptic in $G$. We do not assume $\gamma $ is regular.