Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-20T06:25:05.304Z Has data issue: false hasContentIssue false
  • English
  • Français

Square Integrable Representations and the Standard Module Conjecture for General Spin Groups

Published online by Cambridge University Press:  20 November 2018

Wook Kim
Wook Kim*
Affiliation:
Department of Mathematics, Yonsei University, 134 Shinchondong, Seodaemungu, Seoul, Korea,[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we study square integrable representations and $L$ -functions for quasisplit general spin groups over a 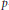$p$-adic field. In the first part, the holomorphy of $L$ -functions in a half plane is proved by using a variant form of Casselman's square integrability criterion and the Langlands–Shahidi method. The remaining part focuses on the proof of the standard module conjecture. We generalize Muić's idea via the Langlands–Shahidi method towards a proof of the conjecture. It is used in the work of M. Asgari and F. Shahidi on generic transfer for general spin groups.

Keywords

11F7011F85
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 61 , Issue 3 , 01 June 2009 , pp. 617 - 640
Copyright
Copyright © Canadian Mathematical Society 2009

References

[1] Asgari, M., Local L-functions for split spinor groups. Canad. J. Math. 54(2002), no. 4, 673–693.Google Scholar
[2] Asgari, M. and Shahidi, F., Generic transfer for general spin groups. Duke Math. J. 132(2006), no. 1, 137–190.Google Scholar
[3] Ban, D., Self-duality in the case of SO(2n, F). Glas. Mat. Ser. III 34(54)(1999), no. 2, 187–196.Google Scholar
[4] Bernstein, I. N. and Zelevinsky, A. V., Induced representations of reductive p-adic groups I. Ann. Sci. É cole Norm. Sup. 10(1977), no. 4, 441–472.Google Scholar
[5] Borel, A., Automorphic L-functions. In: Automorphic forms, representations and L-Functions Part 2, Proc. Sympos. Pure Math 33, American Mathematical Society, Providence, RI, 1979, pp. 27–61.Google Scholar
[6] Borel, A. and Wallach, N., Continuous cohomology, discrete subgroups, and representations of reductive groups. Annals of Mathematics Studies 94, Princeton University Press, Princeton, NJ, 1980.Google Scholar
[7] Casselman, W., Introduction to the theory of admissible representations of p-adic reductive groups. www.math.ubc.ca/-cass/research/pdf/p-adic-book.pdf.Google Scholar
[8] Casselman, W. and Shahidi, F., On irreducibility of standard modules for generic representations. Ann. Sci. École Norm. Sup. 31(1998), no. 4, 561–589.Google Scholar
[9] Cogdell, J. W. and Piatetski-Shapiro, I. I, Converse theorems for GLn. J. Reine Angew. Math. 507(1999), 165–188.Google Scholar
[10] Kim, H., Langlands-Shahidi method and poles of automorphic L-functions: an application to exterior L-functions. Canad. J. Math. 51(1999), no. 4, 835–849.Google Scholar
[11] Kim, H., Functoriality for the exterior square of GL4 and the symmetric fourth of GL2. J. Amer. Math. Soc. 16(2003), no. 1, 139–183.Google Scholar
[12] Kim, H., On local L-functions and normalized intertwining operators. Canad. J. Math. 57(2005), no. 3, 535–597.Google Scholar
[13] Kostant, B., On Whittaker vectors and representation theory. Invent. Math. 48(1978), no. 2, 101–184.Google Scholar
[14] Muić, G., A proof of Casselman-Shahidi's conjecture for quasi-split classical groups. Canad. Math. Bull. 44(2001), no. 3, 298–312.Google Scholar
[15] Rodier, F., Whittaker models for admissible representations of reductive p-adic split groups. In: Harmonic Analysis on Homogeneous Spaces, Proc. Sympos. Pure Math. 26, American Mathematical Society, Providence, RI, 1973, pp. 425–430.Google Scholar
[16] Satake, I., Classification theory of semi-simple algebraic groups. Lecture Notes in Pure Mathematics 3, Marcel Dekker Inc., New York, 1971.Google Scholar
[17] Shahidi, F., On certain L-functions, Amer. J. Math. 103(1981), no. 2, 297–355.Google Scholar
[18] Shahidi, F., Fourier transforms of intertwining operators and Plancherel measures for GL(n). Amer. J. Math. 106(1984), no. 1, 67–111.Google Scholar
[19] Shahidi, F., Local coefficients as Artin factors for real groups. Duke Math J. 52(1985), no. 4, 973–1007.Google Scholar
[20] Shahidi, F., On the Ramanujan conjecture and finiteness of poles for certain L-functions. Ann. of Math. 127(1988), no. 3, 547–584.Google Scholar
[21] Shahidi, F., On the multiplicativity of local factors. In: Festschrift in honor of I. I. Piatetski-Shapiro on the occasion of his sixtieth birthday Part 2, Israel Math. Conf. Proc. 3, Weizmann, Jerusalem, 1990, pp. 279–289.Google Scholar
[22] Shahidi, F., A proof of Langlands conjecture on Plancherel measures; complementary series for p-adic groups. Ann. of Mat. 132(1990), no. 2, 273–330.Google Scholar
[23] Shahidi, F., Twisted endoscopy and reducibility of induced representations for p-adic groups. Duke Math. J. 66(1992), no. 1, 1–41.Google Scholar
[24] Shahidi, F., On non-vanishing of twisted symmetric and exterior square L-functions for GL(n). Pacific J. Math. Special Issue(1997), 311–322.Google Scholar
[25] Silberger, A. J., Introduction to harmonic analysis on reductive p-adic groups. Mathematical Notes 23, Princeton University Press, Princeton, NJ, 1979.Google Scholar
[26] Tadić, M., Representations of p-adic symplectic groups. Compositio Math. 90(1994), no. 2, 123–181.Google Scholar
[27] Tadić, M., On regular square integrable representations of p-adic groups. Amer. J. Math. 120(1998), no. 1, 159–210.Google Scholar
[28] Vogan, D., Gelfand-Kirillov dimension for Harish-Chandra modules. Invent. Math. 48(1978), no. 1, 75–98.Google Scholar
[29] Zelevinsky, A. V., Induced representations of reductive p-adic groups. II. On irreducible representations of GL(n). Ann. Sci. École Norm. Sup. 13(1980), no. 2, 165–210.Google Scholar