Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-12-02T22:49:44.033Z Has data issue: false hasContentIssue false
  • English
  • Français

The Spectral Resolution of Some Non-Selfadjoint Partial Differential Operators

Published online by Cambridge University Press:  20 November 2018

Gustavus E. Huige
Gustavus E. Huige*
Affiliation:
The University of New Brunswick, Saint John, New Brunswick
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

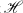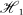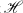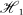Let ffl and be Hilbert spaces, the set of all densely defined linear operators from to , and 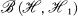its subset of bounded ones. Let 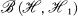and σ(T) denote the adjoint, range, domain, closure and spectrum of T respectively. Ri(z) will denote the resolvent (z — Ti)-1.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 27 , Issue 6 , 01 December 1975 , pp. 1316 - 1322
Copyright
Copyright © Canadian Mathematical Society 1975

References

1. Balslev, E., The singular spectrum of elliptic differential operators in Lp(Rn), Math. Scand. 19 (1966), 193–210.Google Scholar
2. Deic, V. G., A local stationary method in the theory of scattering for a pair of spaces, Soviet Math. Dokl. 12 (1971), 648–652.Google Scholar
3. Goldstein, Ch., Perturbations of non-self adjoint operators I, Arch. Rational Mech. Anal. 37 (1970), 268–296.Google Scholar
4. Greiner, P. C., Eigenfunction expansions and scattering theory for perturbed elliptic partial differential operators, Bull. Amer. Math. Soc. 70 (1964), 517–521.Google Scholar
5. Huige, G. E., Perturbation theory of some spectral operators, Comm. Pure. Appl. Math. 24 (1971), 741–757.Google Scholar
6. Kuroda, S. T., An abstract stationary approach to perturbation of continuous spectra and scattering theory, J. Analyse Math. 20 (1967), 57–117.Google Scholar
7. Martirosjan, R. M., On the spectra of some non-s elf adjoint operators, Amer. Math. Soc. Transi. 53(1966), 81–107.Google Scholar
8. Okikiolu, G. O., Aspects of the theory of bounded integral operators in Lp-spaces (Academic Press, London-New York, 1971).Google Scholar
9. Schechter, M., Spectra of partial differential operators (North-Holland Publishing Co., Amsterdam, 1971).Google Scholar
10. Stankevic, I. V., On the theory of perturbation of a continuous spectrum, Soviet Math. Dokl. 3 (1962), 719–722.Google Scholar
11. Ushijima, T., Spectral theory of the perturbed homogeneous elliptic operator with real constant coefficients, Sci. Papers. College of General Education, University of Tokyo, 16 (1966), 27–42.Google Scholar