Hostname: page-component-669899f699-rg895 Total loading time: 0 Render date: 2025-04-26T11:26:46.674Z Has data issue: false hasContentIssue false
  • English
  • Français

Spectral Properties of the Commutator of Bergman's Projection and the Operator of Multiplication by an Analytic Function

Published online by Cambridge University Press:  20 November 2018

Milutin R. Dostanić
Milutin R. Dostanić*
Affiliation:
Matematički Fakultet, Studentski trg 16, 11000 Beograd, Serbia e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

It is shown that the singular values of the operator 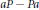$aP\,-\,Pa$, where 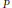$P$ is Bergman's projection over a bounded domain 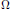$\Omega $ and $a$ is a function analytic on 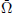$\bar{\Omega }$, detect the length of the boundary of 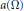$a\left( \Omega \right)$. Also we point out the relation of that operator and the spectral asymptotics of a Hankel operator with an anti-analytic symbol.

Keywords

47B10
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 56 , Issue 2 , 01 April 2004 , pp. 277 - 292
Copyright
Copyright © Canadian Mathematical Society 2004

References

[1] Arazy, J., Fisher, S. D. and Janson, S., An identity for reproducing kernels in a planar domain and Hilbert-Schmidt Hankel operators. J. Reine Angew. Math. 406(1990), 179–199.Google Scholar
[2] Arazy, J., Fisher, S. D. and Peetre, J., Hankel operators on weighted Bergman spaces. Amer. J. Math. 110(1988), 989–1054.Google Scholar
[3] Birman, M. Š. and Solomjak, M. Z., Estimates of singular values of the integral operators. Uspekhi Mat. Nauk (193) 32(1977), 17–84.Google Scholar
[4] Connes, A., Noncommutative Geometry. Academic Press, Inc., 1994.Google Scholar
[5] Dostanić, M. R., Spectral properties of the Cauchy operator and its product with Bergman's projection on a bounded domain. Proc. LondonMath. Soc. (3) 76(1998), 667–684.Google Scholar
[6] Gohberg, I. C. and Krein, M. G., Introduction to the theory of linear nonselfadjoint operators. Transl. Math. Monogr. 18, Amer. Math. Soc., Providence, R.I., 1969.Google Scholar
[7] Itogi nauki i tehniki, Contemporary problems in mathematics, Fundamental directions. 27, Moscow 1988, in Russian.Google Scholar
[8] Leucking, D. H., Characterizations of Certain Classes of Hankel Operators on the Bergman Spaces of the Unit Disk. J. Funct. Anal. 110(1992), 247–271.Google Scholar
[9] Nowak, K., Weak Type Estimate for Singular values of Commutator on Weighted Bergman Spaces. Indiana Univ.Math. J. (4) 40(1991), 1315–1331.Google Scholar
[10] Nowak, M., Compact Hankel operators with conjugate analytic symbols. Rend. Circ. Mat. Palermo (2) 47(1998), 363–374.Google Scholar
[11] Paraska, V. I., On asymptotics of eigenvalues and singular numbers of linear operators which increase smoothness. In: Russian Math. Sb. (NS) 68(1965), 623–631.Google Scholar
[12] Range, R. M., Holomorphic functions and integral representations in several complex variables. Springer, Berlin, 1986.Google Scholar
[13] Warschawski, S. E., Über das Randverhalten der Ableitung der Abbildungs-funktion bei konformer Abbildung. Math. Z. (3–4) 35(1932), 321–456.Google Scholar
[14] Zhy, K., OperatorTheory in Function Spaces. Marcel Dekker INC., 1990.Google Scholar