Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-25T05:59:07.487Z Has data issue: false hasContentIssue false
  • English
  • Français

A Specialised Net of Quadrics Having Selfpolar Polyhedra, with Details of the Fivedimensional Example

Published online by Cambridge University Press:  20 November 2018

W. L. Edge
W. L. Edge*
Affiliation:
Inveresk House, Musselburgh, Scotland
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

If x0,x1, … xn are homogeneous coordinates in [n], projective space of n dimensions, the prime (to use the standard name for a hyperplane)

osculates, as θ varies, the rational normal curve C whose parametric form is [2, p. 347]

Take a set of n + 2 points on C for which θ = ηjζ where ζ is any complex number and

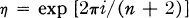
so that the ηj, for 0 ≦ j < n + 2, are the (n + 2)th roots of unity. The n + 2 primes osculating C at these points bound an (n + 2)-hedron H which varies with η, and H is polar for all the quadrics

(1.1)

in the sense that the polar of any vertex, common to n of its n + 2 bounding primes, contains the opposite [n + 2] common to the residual pair.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 33 , Issue 4 , 01 August 1981 , pp. 885 - 892
Copyright
Copyright © Canadian Mathematical Society 1981

References

1. Baker, H. F., Principles of geometry, Vol. VI (Cambridge, 1933).Google Scholar
2. Bertini, E., Introduzione alia geometria proiettiva degli iperspazi (Messina, 1923).Google Scholar
3. Edge, W. L., A special net of quadrics, Proc. Edinburgh Math. Soc. (2) 4 (1936), 185–209.Google Scholar
4. Edge, W. L., Notes on a net of quadric surfaces V: The pentahedral net, Proc. London Math. . Soc. (2) 47 (1942), 455–480.Google Scholar
5. Edge, W. L., A special polyhedral net of quadrics, Journal London Math. Soc. (2) 22 (1980), 46–56.Google Scholar