Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-28T17:27:37.918Z Has data issue: false hasContentIssue false
  • English
  • Français

Special Abelian Group Difference Sets

Published online by Cambridge University Press:  20 November 2018

E. C. Johnsen
E. C. Johnsen*
Affiliation:
University of California, Santa Barbara, California
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A 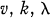abelian group difference set (abbreviated AGDS) (G, D) is a 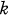-subset D = {di}1k taken from an abelian group G of order v such that each element different from the identity e in G appears exactly λ times in the set of differences {didj-1}, where 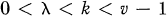. Combinatorially, 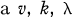AGDS is equivalent to a 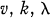design having an abelian collineation group which is transitive and regular on the elements and on the blocks of the design (1).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 20 , 1968 , pp. 1269 - 1275
Copyright
Copyright © Canadian Mathematical Society 1968

Footnotes

This paper was presented to the American Mathematical Society at the Annual Meeting in Chicago, Illinois, January 25, 1966. This work was supported by Air Force Office of Scientific Research Grants AFOSR 698-65 and 698-67.

References

1. Bruck, R. H., Difference sets in a finite group, Trans. Amer. Math. Soc. 78 (1955), 464–481.Google Scholar
2. Johnsen, E. C., The inverse multiplier for abelian group difference sets, Can. J. Math. 16 1964), 787–796.Google Scholar
3. Johnsen, E. C., Skew-Hadamard abelian group difference sets, J. Algebra 4 (1966), 388–402.Google Scholar
4. McFarland, Robert and Mann, H. B., On multipliers of difference sets, Can. J. Math. 17 1965), 541–542.Google Scholar
5. Ryser, H. J., A note on a combinatorial problem, Proc. Amer. Math. Soc. 1 (1950), 422–424.Google Scholar