Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-27T23:58:20.642Z Has data issue: false hasContentIssue false
  • English
  • Français

Spaces of Lorentz Multipliers

Published online by Cambridge University Press:  20 November 2018

Kathryn E. Hare  and
Enji Sato
Kathryn E. Hare
Affiliation:
Dept. of Pure Mathematics Univ. of Waterloo Waterloo, Ont. N2L 3G1, email: [email protected]
Enji Sato
Affiliation:
Dept. of Mathematical Sciences Faculty of Science Yamagata University Yamagata 990-8560 Japan, email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study when the spaces of Lorentz multipliers from 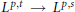${{L}^{p,t\,}}\to \,{{L}^{p,s}}$ are distinct. Our main interest is the case when 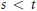$s\,<\,t$, the Lorentz-improving multipliers. We prove, for example, that the space of multipliers which map 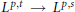${{L}^{p,t\,}}\to \,{{L}^{p,s}}$ is different from those mapping 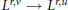${{L}^{r,v}}\,\to \,{{L}^{r,u}}$ if either 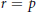$r\,=\,p$ or 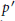${p}'$ and 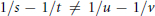$1/s\,-\,1/t\,\ne \,1/u\,-\,1/v$, or 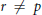$r\,\ne \,p$ or 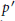${p}'$. These results are obtained by making careful estimates of the Lorentz multiplier norms of certain linear combinations of Fejer or Dirichlet kernels. For the case when the first indices are different the linear combination we analyze is in the spirit of a Rudin-Shapiro polynomial.

Keywords

43A2242A4546E30multipliersconvolution operatorsLorentz spacesLorentz-improving multipliers
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 53 , Issue 3 , 01 June 2001 , pp. 565 - 591
Copyright
Copyright © Canadian Mathematical Society 2001

References

[1] Bak, J.-G., Sharp convolution estimates for measures on flat surfaces. J. Math. Anal. Appl. 193 (1995), 756–771.Google Scholar
[2] Bak, J.-G., McMichael, J. and Oberlin, D., Convolution estimates for some measures on flat curves. J. Funct. Anal. 101 (1991), 81–96.Google Scholar
[3] Christ, M., A convolution inequality concerning Cantor-Lebesgue measures. Rev. Mat. Iberoamericana 1 (1985), 79–83.Google Scholar
[4] Cowling, M. and J. Fournier, Inclusions and noninclusion of spaces of convolution operators. Trans. Amer.Math. Soc. 221 (1976), 59–95.Google Scholar
[5] Gaudry, G., Bad behavior and inclusion results for multipliers of type (p,q). Pacific J. Math. 35 (1970), 83–94.Google Scholar
[6] Graham, C., Hare, K. and Ritter, D., The size of Lp-improving measures. J. Funct. Anal. 84 (1989), 472–495.Google Scholar
[7] Grinnell, R., Lorentz-improving measures on compact abelian groups. Ph.D. Dissertation, Queen's University, 1991.Google Scholar
[8] Grinnell, R. and Hare, K., Lorentz-improving measures. Illinois J. Math. 38 (1994), 366–389.Google Scholar
[9] Hare, K., Properties and examples of (Lp, Lq) multipliers. Indiana Univ. Math. J. 38 (1989), 211–227.Google Scholar
[10] Hunt, R., On L(p,q) spaces. Enseign. Math. 12 (1966), 249–276.Google Scholar
[11] O’Neil, R., Convolution operators and L(p,q) spaces. Duke Math. J. 30 (1963), 129–142.Google Scholar
[12] Price, J., Some strict inclusions between spaces of Lp multipliers. Trans. Amer. Math. Soc. 152 (1970), 321–330.Google Scholar
[13] Ritter, D., Most Riesz product measures are Lp-improving. Proc. Amer.Math. Soc. 97 (1986), 291–295.Google Scholar
[14] Sagher, Y., An application of interpolation theory to Fourier series. Studia Math. 61 (1972), 169–181.Google Scholar
[15] Zafran, M., Multiplier transformations of weak type. Ann. of Math. 101 (1975), 34–44.Google Scholar