Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-30T19:10:54.671Z Has data issue: false hasContentIssue false
  • English
  • Français

Some Results on the Center of an Algebra of Operators on VN(G) for the Heisenberg group

Published online by Cambridge University Press:  20 November 2018

C. Cecchini  and
A. Zappa
C. Cecchini
Affiliation:
Universitá di Genova, Genova, Italy
A. Zappa
Affiliation:
Universitá di Genova, Genova, Italy
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let G be an amenable locally compact group. We will use the terminology of [3] and denote by VN(G) the Von Neumann algebra of the regular representation and by A(G) its predual, which is the algebra of the coefficients of the regular representation. The Von Neumann algebra VN(G) is, in a natural fashion, a module with respect to A(G) [3].

The algebra 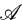of bounded linear operators on VN(G), which commute with the action of A(G), has been studied in [6] and in [1]. If UCB(Ĝ) is the space of the elements of VN(G) of the form vT, for some v in A(G) and some T in VN(G) (see for instance [4]), in [6] and in [1] it is proved that, for any amenable locally compact group there exists an isometric bijection between 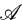and UCB(Ĝ)*.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 33 , Issue 6 , 01 December 1981 , pp. 1469 - 1486
Copyright
Copyright © Canadian Mathematical Society 1981

References

1. Cecchini, C., Operators on VN(G) commuting with A(G), to appear in Colloquium Mathematicum.Google Scholar
2. Dixmier, J., Les C*-algèbres et leur représentations, (Gauthier-Villars, Paris, 1969).Google Scholar
3. Eymard, P., L'algèbre de Fourier d'un groupe locallement compact, Bull. Soc. Math. France 92 (1964), 181–236.Google Scholar
4. Granirer, E., Weakly almost periodic and uniformly continuous junctionals on the Fourier algebra of any locally compact group, Trans. A. M. S. 189 (1974), 371–382.Google Scholar
5. Granirer, E., Density theorems for some linear subspaces, Symposia Math. 22 (1977), 61–70.Google Scholar
6. Lau, A. T., Uniformly continuous Junctionals on the Fourier algebra of any locally compact group, Trans. A. M. S. 251 (1979), 39–59.Google Scholar
7. Mackey, G. W., The theory of unitary group representations, (The University of Chicago Press, Chicago and London, 1976).Google Scholar
8. Nakamura, M. and Umegaki, H., Heisenberg's commutation relation and the Plancherel theorem, Proc. Japan Acad. 37 (1961), 239–242.Google Scholar
9. Pukanszky, L., Leçons sur les représentations des groupes, (Dunod, Paris, 1967).Google Scholar
10. Zappa, A., The center of the convolution algebra CU *(G), Rend. Sem. Univ. Padova 52 (1974), 71–83.Google Scholar