Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-12-03T20:30:03.577Z Has data issue: false hasContentIssue false
  • English
  • Français

Some Open Sets for Which the Heat Equation is Simplicial

Published online by Cambridge University Press:  20 November 2018

Peter D. Taylor
Peter D. Taylor*
Affiliation:
Queen's University, Kingston, Ontario
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let us associate to each open set U ⊂ Rn+1 the space HU of real functions f which are twice continuously differentiable in x1 . . . xn and once continuously differentiable in xn+1 and which satisfy the heat equation: Δf = ∂f/∂xn+1 where 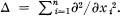Then we have what in the axiomatic of Bauer is called a strong harmonic space [2, p. 61]. We will call functions of HUharmonic in U.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 26 , Issue 2 , April 1974 , pp. 455 - 472
Copyright
Copyright © Canadian Mathematical Society 1974

References

1. Alfsen, E. M. and Andersen, T. B., Split faces of compact convex sets, Proc. London Math. Soc. 21 (1970), 415–42.Google Scholar
2. Bauer, H., Harmonische Raume und ihre Potentialtheorie, Lecture Notes in Math. 22 (Springer-Verlag, 1966).Google Scholar
3. Effros, E. G. and Kazdan, J. L., Applications of Choquet simplexes to elliptic and parabolic boundary value problems, J. Differential Equations 8 (1970), 95–134.Google Scholar
4. Edwards, D. A., Separation des fonctions réelles définies sur un simplexe de Choquet, C. R. Acad. Sci. Paris, Sér. A-B 261 (1965), 2798–2800.Google Scholar
5. Jellett, F., Homomorphisms and inverse limits of Choquet simplexes, Math. Z. 108 (1968), 219–226.Google Scholar
6. Phelps, R. R., Lectures on Choquet's Theorem (Van Nostrand, Princeton, 1966).Google Scholar
7. Alfsen, E. M., Compact convex sets and boundary integrals, Ergebnisse der Mathematik und ihrer Grenzgebiete 57 (Springer-Verlag, 1971).Google Scholar
8. Ellis, A. J., On faces of compact convex sets and their annihilators, Math. Ann. 184 (1969), 19–24.Google Scholar
9. Boboc, N. and Cornea, A., Convex cones of lower semicontinuous functions, Rev. Roumaine. Math. Pures Appl. 12 (1967), 471–525.Google Scholar
10. Kohn, J. and Sieveking, M., Regulare und extremale Randpunkte in der Potentialtheorie, Rev. Roumaine Math. Pures Appl. 12 (1967), 1489–1502.Google Scholar
11. Kelley, J. L., General topology (Van Nostrand, Princeton, 1955).Google Scholar
12. Semadeni, Z., Banach spaces of continuous functions, Vol. I, Monografie Matematyczne, PWN (Warszawa, Poland, 1971).Google Scholar
13. Davies, E. B. and Vincent, G. F.-Smith, Tensor products, infinite products, and projective limits of Choquet simplexes, Math. Scand. 22 (1968), 145–164.Google Scholar
14. Effros, E. G., Structure in simplexes, Acta Math. 117 (1967), 103–121.Google Scholar