Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-18T11:04:04.711Z Has data issue: false hasContentIssue false
  • English
  • Français

Some New Results on L2 Cohomology of Negatively Curved Riemannian Manifolds

Published online by Cambridge University Press:  20 November 2018

M. Cocos
M. Cocos*
Affiliation:
Department of Mathematics, University of Minnesota, Minneapolis, Minnesota 55455, U.S.A., e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The present paper is concerned with the study of the 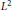${{L}^{2}}$ cohomology spaces of negatively curved manifolds. The first half presents a finiteness and vanishing result obtained under some curvature assumptions, while the second half identifies a class of metrics having non-trivial 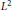${{L}^{2}}$ cohomology for degree equal to the half dimension of the space. For the second part we rely on the existence and regularity properties of the solution for the heat equation for forms.

Keywords

58J50
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 57 , Issue 2 , 01 April 2005 , pp. 251 - 266
Copyright
Copyright © Canadian Mathematical Society 2005

References

[1] Browder, F. E., Eigenfunction expansion for singular elliptic operators. Proc. Nat. Acad. Sci. U.S.A. 42(1954), 459–463.Google Scholar
[2] Cheeger, J., On the Hodge theory of Riemannian pseudomanifolds. In: Geometry of the Laplace Operator, Proc. Sympos. Pure Math. 36, Amer.Math. Soc., Providence, 1980, pp. 91–146.Google Scholar
[3] de Rham, G., Variétés Differentiables. Hermann, Paris, 1973.Google Scholar
[4] Dodziuk, J., L2 harmonic forms on complete manifolds. In: Seminar on Differential Geometry, Ann. of Math. Stud. 102, Princeton University Press, Princeton, NJ, 1982, pp. 291–302.Google Scholar
[5] Dodziuk, J., L2 harmonic forms on rotationally symmetric Riemannian manifolds. Proc. Amer.Math. Soc. 77(1979), 395–400.Google Scholar
[6] Donnelly, H., Xavier, F., On the differential form spectrum of negatively curved Riemannian manifolds. Amer. J. Math. 106(1984), 169–185.Google Scholar
[7] Elworthy, K. D., Xue-Mei Li and Steven Rosenberg, Bounded and L2 harmonic forms on universal covers. Geom. Funct. Anal. 8(1998), 283–303.Google Scholar
[8] Gaffney, M., The harmonic operator for exterior differential forms. Proc. Nat. Acad. Sci. U.S.A. 37(1951), 48–50.Google Scholar
[9] Gromov, M., Kähler hyperbolicity and L2-Hodge theory. J. Differential Geom. 33(1991), 263–292.Google Scholar
[10] Hatcher, A., Algebraic Topology. Cambridge University Press, Cambridge, 2002.Google Scholar
[11] Hitchin, N., L2-cohomology of hyperkähler quotients. Comm. Math. Phys. 211(2000), 153–165.Google Scholar
[12] Jost, J., Riemannian Geometry and Geometric Analysis. Springer-Verlag, Berlin, 1995.Google Scholar
[13] McKean, H., An upper bound to the spectrum of the Δ on a manifold of negative curvature. J. Differential Geom. 4(1970), 359–366.Google Scholar
[14] Rosenberg, S., The Laplacian on a Riemannian Manifold. Cambridge University Press, Cambridge, 1997.Google Scholar
[15] Segal, G. and Selby, A., The cohomology of the space of magnetic monopoles. Comm. Math. Phys. 177(1996), 775–787.Google Scholar
[16] Singer, I., Some remarks on operator theory and index theory. Springer Lecture Notes Math. 575(1977), 128–138.Google Scholar
[17] Teleman, N., Combinatorial Hodge theory and signature theorem.In: Geometry of the Laplace operator. Proc. Sympos. Pure Math. 36, Amer.Math. Soc., Providence, RI, 1980, pp. 287–292.Google Scholar
[18] Vesentini, E., Lectures on Levi convexity of complex manifolds and cohomology vanishing theorems. Tata Inst. of Fund. Research, Bombay, 1967.Google Scholar