Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-24T09:42:43.902Z Has data issue: false hasContentIssue false
  • English
  • Français

Some Extreme Rays of the Positive Pluriharmonic Functions

Published online by Cambridge University Press:  20 November 2018

Frank Forelli
Frank Forelli*
Affiliation:
The University of Wisconsin – Madison, Madison, Wisconsin
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

1.1. We will denote by B the open unit ball in Cn, and we will denote by H(B) the class of all holomorphic functions on B. Let

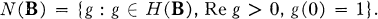
Thus N(B) is convex (and compact in the compact open topology). We think that the structure of N(B) is of interest and importance. Thus we proved in [1] that if

(1.1)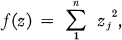

if

(1.2)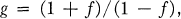

and if n≧ 2, then g is an extreme point of N(B). We will denote by E(B) the class of all extreme points of N(B). If n = 1 and if (1.2) holds, then as is well known g ∈ E(B) if and only if

(1.3)

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 31 , Issue 1 , 01 February 1979 , pp. 9 - 16
Copyright
Copyright © Canadian Mathematical Society 1979

References

1. Forelli, F., Measures whose Poisson integrals are pluriharmonic II, Illinois J. Math. 19 (1975), 584–592.Google Scholar
2. Forelli, F., A necessary condition on the extreme points of a class of holomorphic functions, Pacific J. Math. 73 (1977), 81–86.Google Scholar