Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-28T01:10:11.851Z Has data issue: false hasContentIssue false
  • English
  • Français

Some complexity results in the theory of normal numbers

Part of: Probabilistic theory: distribution modulo $1$; metric theory of algorithms Set theory Number theory: Connections with logic

Published online by Cambridge University Press:  28 September 2020

Dylan Airey ,
Steve Jackson  and
Bill Mance
Dylan Airey
Affiliation:
Department of Mathematics, Princeton University, Fine Hall, Washington Road, Princeton, NJ08544-1000, USAe-mail:[email protected]
Steve Jackson*
Affiliation:
Department of Mathematics, University of North Texas, General Academics Building 435, 1155 Union Circle, Denton, #311430, TX76203-5017, USA
Bill Mance
Affiliation:
Uniwersytet im. Adama Mickiewicza w Poznaniu, Collegium Mathematicum, ul. Umultowska 87, Poznań61-614, Polande-mail:[email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

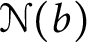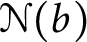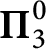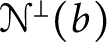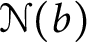Let $\mathcal {N}(b)$ be the set of real numbers that are normal to base b. A well-known result of Ki and Linton [19] is that $\mathcal {N}(b)$ is $\boldsymbol {\Pi }^0_3$ -complete. We show that the set ${\mathcal {N}}^\perp (b)$ of reals, which preserve $\mathcal {N}(b)$ under addition, is also 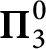$\boldsymbol {\Pi }^0_3$ -complete. We use the characterization of 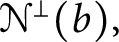${\mathcal {N}}^\perp (b),$ given by Rauzy, in terms of an entropy-like quantity called the noise. 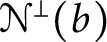It follows from our results that no further characterization theorems could result in a still better bound on the complexity of ${\mathcal {N}}^\perp (b)$ . We compute the exact descriptive complexity of other naturally occurring sets associated with noise. One of these is complete at the 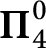$\boldsymbol {\Pi }^0_4$ level. Finally, we get upper and lower bounds on the Hausdorff dimension of the level sets associated with the noise.

Keywords

normal numbersnoisecomplexity

MSC classification

Primary: 03E15: Descriptive set theory 11K16: Normal numbers, radix expansions, Pisot numbers, Salem numbers, good lattice points, etc.
Secondary: 11U99: None of the above, but in this section
Type
Article
Information
Canadian Journal of Mathematics , Volume 74 , Issue 1 , February 2022 , pp. 170 - 198
Check for updates
Copyright
© Canadian Mathematical Society 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first author was supported by the National Science Foundation Graduate Research Fellowship grant DGE-1656466. The second author was supported by NSF grant DMS-1800323. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation. The authors wish to thank the referee for several suggestions which significantly improved the paper.

References

Agafonov, V. N., Normal sequences and finite automata. Dokl. Akad. Nauk SSSR 179(1968), 255–256.Google Scholar
Airey, D., Jackson, S., Kwietniak, D., and Mance, B., Borel complexity of sets of normal numbers via generic points in subshifts with specification. Trans. Am. Math. Soc. 373(2020), 4561–4854.CrossRefGoogle Scholar
Airey, D., Jackson, S., Kwietniak, D., and Mance, B., Borel complexity of the set of generic points of dynamical systems with a specification property. In preparation, 2020.CrossRefGoogle Scholar
Airey, D. and Mance, B., Normality preserving operations for Cantor series expansions and associated fractals, I. Illinois J. Math. 3(2015), 531–543.Google Scholar
Airey, D., Mance, B., and Vandehey, J., Normality preserving operations for Cantor series expansions and associated fractals II. N. Y. J. Math. 21(2015), 1311–1326.Google Scholar
Aistleitner, C., On modifying normal numbers. Unif. Distrib. Theory 6(2011), no. 2, 49–58.Google Scholar
Becher, V., Heiber, P. A., and Slaman, T. A., Normal numbers and the Borel hierarchy. Fundam. Math. 226(2014), no. 1, 63–78.CrossRefGoogle Scholar
Becher, V. and Slaman, T. A., On the normality of numbers to different bases. J. Lond. Math. Soc. 90(2014), no. 2, 472–494.CrossRefGoogle Scholar
Bernay, M., La dimension de Hausdorff de l’ensemble des nombres r-déterministes. C. R. Acad. Sci. Paris 280(1975), A539–A541.Google Scholar
Beros, K. A., Normal numbers and completeness results for difference sets. J. Symb. Log. 82(2017), no. 1, 247–257.CrossRefGoogle Scholar
Chang, K. T., A note on normal numbers. Nanta Math. 9(1976), 70–72.Google Scholar
Colebrook, C. M., The Hausdorff dimension of certain sets of nonnormal numbers. Mich. Math. J. 17(1970), 103–116.CrossRefGoogle Scholar
Doty, D., Lutz, J. H., and Nandakumar, S., Finite-state dimension and real arithmetic. Inf. Comput. 205(2007), 1640–1651.CrossRefGoogle Scholar
Furstenberg, H., Disjointness in Ergodic theory, minimal sets, and a problem in diophantine approximation. Math. Syst. Theory 1(1967), 1–49.CrossRefGoogle Scholar
Heersink, B. and Vandehey, J., Continued fraction normality is not preserved along arithmetic progressions. Arch. Math. (Basel), 106(2016), no. 4, 363–370.CrossRefGoogle Scholar
Kamae, T., Subsequences of normal sequences. Israel J. Math. 16(1973), 121–149.CrossRefGoogle Scholar
Kamae, T. and Weiss, B., Normal numbers and selection rules. Israel J. Math. 21(1975), 101–110.CrossRefGoogle Scholar
Kechris, A., Classical descriptive set theory. Graduate Texts in Mathematics, 156, Springer-Verlag, New York, NY, 1995.CrossRefGoogle Scholar
Ki, H. and Linton, T., Normal numbers and subsets of N with given densities. Fundam. Math. 144(1994), no. 2, 163–179.Google Scholar
Kuipers, L. and Niederreiter, H., Uniform distribution of sequences. Dover, Mineola, NY, 2006.Google Scholar
Mauduit, C., Problem session dedicated to Gérard Rauzy. In: Dynamical systems (Luminy–Marseille, 1998). World Scientific Publishing, River Edge, NJ, 2000.Google Scholar
Merkle, W. and Reimann, J., Selection functions that do not preserve normality. Theory Comput. Syst. 39(2006), no. 5, 685–697.CrossRefGoogle Scholar
Rauzy, G., Nombres normaux et processus déterministes. Acta Arith. 29(1976), no. 3, 211–225.CrossRefGoogle Scholar
Vandehey, J., Non-trivial matrix actions preserve normality for continued fractions. 153(2015), no. 2, 274–293. arXiv:1504.05121Google Scholar
Wall, D. D., Normal numbers. Ph.D. thesis, University of California, Berkeley, Berkeley, CA, 1949.Google Scholar