No CrossRef data available.
Article contents
S-Maximal Subgroups of πl(M3)
Published online by Cambridge University Press: 20 November 2018
Extract
Let M be a compact, connected, irreducible 3-manifold. Let S be a closed, connected, 2-manifold other than the 2-sphere or projective plane. Let f be a map of S into M such that
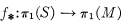
Suppose for every closed, connected surface S1 and every map g:S1 → M such that
(1) 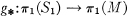 is an injection,
is an injection,
(1)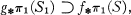
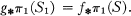 Then we shall say that the subgroup
Then we shall say that the subgroup 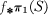 is a surface maximal or S-maximal subgroup of π1(M). We may also say that the map f is S-maximal.
is a surface maximal or S-maximal subgroup of π1(M). We may also say that the map f is S-maximal.
Let M be an irreducible 3-manifold which does not admit any embedding of the projective plane. Then we shall say that M is p2-irreducible. Throughout this paper all spaces will be simplicial complexes and all maps will be piecewise linear.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1972


