Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-24T06:46:20.532Z Has data issue: false hasContentIssue false
  • English
  • Français

Small Coverings with Smooth Functions under the Covering Property Axiom

Published online by Cambridge University Press:  20 November 2018

Krzysztof Ciesielski  and
Janusz Pawlikowski
Krzysztof Ciesielski
Affiliation:
Department of Mathematics, West Virginia University, Morgantown, WV 26506-6310, U.S.A., e-mail: [email protected]
Janusz Pawlikowski
Affiliation:
Department of Mathematics, University of Wrocław, pl. Grunwaldzki 2/4, 50-384 Wrocław, Poland, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In the paper we formulate a Covering Property Axiom, 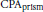$\text{CP}{{\text{A}}_{\text{prism}}}$, which holds in the iterated perfect set model, and show that it implies the following facts, of which (a) and (b) are the generalizations of results of J. Steprāns.

(a) There exists a family 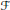$\mathcal{F}$ of less than continuum many 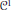${{C}^{1}}$ functions from 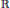$\mathbb{R}$ to 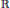$\mathbb{R}$ such that 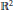${{\mathbb{R}}^{2}}$ is covered by functions from 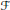$\mathcal{F}$, in the sense that for every 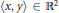$\left\langle x,\,y \right\rangle \,\in \,{{\mathbb{R}}^{2}}$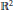${{\mathbb{R}}^{2}}$ there exists an 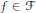$f\,\in \,\mathcal{F}$ such that either 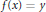$f\left( x \right)\,=\,y$ or 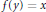$f\left( y \right)\,=\,x$.

(b) For every Borel function 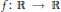$f:\,\mathbb{R}\,\to \,\mathbb{R}$ there exists a family 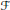$\mathcal{F}$ of less than continuum many “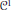${{C}^{1}}$” functions (i.e., differentiable functions with continuous derivatives, where derivative can be infinite) whose graphs cover the graph o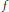f $f$.

(c) For every 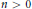$n\,>\,0$ and a 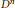${{D}^{n}}$ function 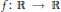$f:\,\mathbb{R}\,\to \,\mathbb{R}$ there exists a family 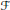$\mathcal{F}$ of less than continuum many 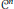${{C}^{n}}$ functions whose graphs cover the graph o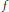f $f$.

We also provide the examples showing that in the above properties the smoothness conditions are the best possible. Parts (b), (c), and the examples are closely related to work of A. Olevskiî.

Keywords

26A2403E35continuoussmoothcovering
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 57 , Issue 3 , 01 June 2005 , pp. 471 - 493
Copyright
Copyright © Canadian Mathematical Society 2005

References

[1] Agronsky, S., Bruckner, A. M., Laczkovich, M., and Preiss, D., Convexity conditions and intersections with smooth functions. Trans. Amer.Math. Soc. 289(1985), 659–677.Google Scholar
[2] Bartoszy, T. ński, Judah, H., Set Theory. A K Peters, Wellesley, MA, 1995.Google Scholar
[3] Brown, J. B., Differentiable restrictions of real functions. Proc. Amer.Math. Soc. 108(1990), 391–398.Google Scholar
[4] Brown, J. B., Restriction theorems in real analysis. Real Anal. Exchange 20(1994/95), 510–526.Google Scholar
[5] Bruckner, A. M., Differentiation of Real Functions. CRM Monograph Series 5, American Mathematical Society, Providence, RI, 1994.Google Scholar
[6] Burges, J. P., A selector principle forΣ1 1 equivalence relations. Michigan Math. J. 24(1977), 65–76.Google Scholar
[7] Cichoń, J., Morayne, M., Pawlikowski, J., and Solecki, S., Decomposing Baire functions. J. Symbolic Logic 56(1991), 1273–1283.Google Scholar
[8] Ciesielski, K., Set theoretic real analysis. J. Appl. Anal. 3(1997), 143–190. Available at http://www.math.wvu.edu./˜kcies/STA/STA.html.Google Scholar
[9] Ciesielski, K., Set Theory for theWorking Mathematician. LondonMathematical Society Student Texts 39, Cambridge University Press, Cambridge, 1997.Google Scholar
[10] Ciesielski, K., Decomposing symmetrically continuous functions and Sierpiński-Zygmund functions into continuous functions. Proc. Amer.Math. Soc. 127(1999), 3615–3622. Available at http://www.math.wvu.edu./˜kcies/STA/STA.html.Google Scholar
[11] Ciesielski, K. and Natkaniec, T., On Sierpiński-Zygmund bijections and their inverses. Topology Proc. 22(1997), 155–164. Available at http://www.math.wvu.edu./˜kcies/STA/STA.html.Google Scholar
[12] Ciesielski, K. and Pawlikowski, J., Crowded and selective ultrafilters under the covering property axiom. J. Appl. Anal. 9(2003), 19–55. Available at http://www.math.wvu.edu./˜kcies/STA/STA.html.Google Scholar
[13] Ciesielski, K. and Pawlikowski, J., Covering Property Axiom CPA. A Combinatorial Core of the Iterated Perfect Set Model. Cambridge Tracts in Mathematics 164, Cambridge University Press, Cambridge, 2004.Google Scholar
[14] Ciesielski, K., and Wojciechowski, J., Sums of connectivity functions on Rn. Proc. LondonMath. Soc. (3) 76(1998), 406–426. Available at http://www.math.wvu.edu./˜kcies/STA/STA.html.Google Scholar
[15] Federer, H., Geometric measure theory. Die Grundlehren der mathematischenWissenschaften 153, Springer-Verlag, New York 1969.Google Scholar
[16] Galvin, F., Partition theorems for the real line. Notices Amer.Math. Soc. 15 (1968), 660.Google Scholar
[17] Galvin, F., Errata to “Partition theorems for the real line”. Notices Amer.Math. Soc. 16 (1969), 1095.Google Scholar
[18] Engelking, R., General Topology. Polish Scientific Publishers, Warsaw, 1977.Google Scholar
[19] Kanovei, V., Non-Glimm–Effros equivalence relations at second projective level. Fund. Math. 154(1997), 1–35.Google Scholar
[20] Kechris, A. S., Classical Descriptive Set Theory. Graduate Texts in mathematics 156, Springer-Verlag, New York, 1995.Google Scholar
[21] Mauldin, R. D., The Scottish Book. Birkhäuser, Boston, 1981.Google Scholar
[22] Miller, A.W., Mapping a set of reals onto the reals. J. Symbolic Logic 48(1983), 575–584.Google Scholar
[23] Morayne, M., On continuity of symmetric restrictions of Borel functions. Proc. Amer.Math. Soc. 98(1985), 440–442.Google Scholar
[24] Olevskiĭ, A., Ulam-Zahorski problem on free interpolation by smooth functions. Trans. Amer. Math. Soc. 342(1994), 713–727.Google Scholar
[25] Steprāns, J., Sums of Darboux and continuous functions, Fund. Math. 146(1995), 107–120.Google Scholar
[26] Steprāns, J., Decomposing Euclidean space with a small number of smooth sets. Trans. Amer. Math. Soc. 351(1999), 1461–1480.Google Scholar
[27] Ulam, S., A Collection of Mathematical Problems. Interscience Tracts in Pure and Applied Mathematics 8, New York, Interscience, 1960.Google Scholar
[28] Whitney, H., Analytic extensions of differentiable functions defined in closed sets. Trans. Amer.Math. Soc. 36(1934), 63–89.Google Scholar
[29] Zahorski, Z., Sur l’ensamble des points singuliers d’une fonction d’une variable réele admettant les dérivées des tous ordres, Fund. Math. 34(1947), 183–245.Google Scholar