Hostname: page-component-6587cd75c8-cpvbf Total loading time: 0 Render date: 2025-04-23T20:11:56.300Z Has data issue: false hasContentIssue false
  • English
  • Français

Sliding methods for tempered fractional parabolic problem

Part of: Parabolic equations and systems Miscellaneous topics - Partial differential equations Partial differential equations

Published online by Cambridge University Press:  28 July 2023

Shaolong Peng
Shaolong Peng*
Affiliation:
Academy of Mathematics and Systems Science, Chinese Academy of Sciences, Beijing 100190, China
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this article, we are concerned with the tempered fractional parabolic problem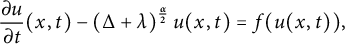

$$ \begin{align*}\frac{\partial u}{\partial t}(x, t)-\left(\Delta+\lambda\right)^{\frac{\alpha}{2}} u(x, t)=f(u(x, t)), \end{align*} $$

where 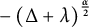$-\left (\Delta +\lambda \right )^{\frac {\alpha }{2}}$ is a tempered fractional operator with 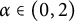$\alpha \in (0,2)$ and 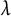$\lambda $ is a sufficiently small positive constant. We first establish maximum principle principles for problems involving tempered fractional parabolic operators. And then, we develop the direct sliding methods for the tempered fractional parabolic problem, and discuss how they can be used to establish monotonicity results of solutions to the tempered fractional parabolic problem in various domains. We believe that our theory and methods can be conveniently applied to study parabolic problems involving other nonlocal operators.

Keywords

Tempered fractional parabolic problemmaximum principlesliding methodsmonotonicity

MSC classification

Primary: 35K55: Nonlinear parabolic equations
Secondary: 35B30: Dependence of solutions on initial and boundary data, parameters 35R11: Fractional partial differential equations
Type
Article
Information
Canadian Journal of Mathematics , Volume 76 , Issue 4 , August 2024 , pp. 1358 - 1378
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

Shaolong Peng is supported by the NSFC (Grant No. 11971049).

References

Berestycki, H. and Nirenberg, L., Some qualitative properties of solutions of semilinear elliptic equations in cylindrical domains . In: Analysis, et Cetera, Academic Press, Boston, MA, 1990, pp. 115–164.10.1016/B978-0-12-574249-8.50011-0CrossRefGoogle Scholar
Berestycki, H. and Nirenberg, L., On the method of moving planes and the sliding method . Bol. Soc. Brasil. Mat. (N.S.) 22(1991), 1–37.10.1007/BF01244896CrossRefGoogle Scholar
Bertoin, J., Lévy processes, Cambridge Tracts in Mathematics, 121, Cambridge University Press, Cambridge, 1996.Google Scholar
Cabré, X. and Tan, J., Positive solutions of nonlinear problems involving the square root of the Laplacian . Adv. Math. 224(2010), 2052–2093.10.1016/j.aim.2010.01.025CrossRefGoogle Scholar
Caffarelli, L. and Silvestre, L., An extension problem related to the fractional Laplacian . Comm. PDEs 32(2007), 1245–1260.10.1080/03605300600987306CrossRefGoogle Scholar
Caffarelli, L. and Vasseur, L., Drift diffusion equations with fractional diffusion and the quasi-geostrophic equation . Ann. of Math. 171(2010), no. 3, 1903–1930.10.4007/annals.2010.171.1903CrossRefGoogle Scholar
Cao, D., Dai, W., and Qin, G., Super poly-harmonic properties, Liouville theorems and classification of nonnegative solutions to equations involving higher-order fractional Laplacians . Trans. Amer. Math. Soc. 374(2021), no. 7, 4781–4813.10.1090/tran/8389CrossRefGoogle Scholar
Chen, W. and Hu, Y., Monotonicity of positive solutions for nonlocal problems in unbounded domains. J. Funct. Anal. 281(2021), Article ID: 109187.10.1016/j.jfa.2021.109187CrossRefGoogle Scholar
Chen, W., Li, C., and Li, Y., A direct method of moving planes for the fractional Laplacian. Adv. Math. 308(2017), 404–437.10.1016/j.aim.2016.11.038CrossRefGoogle Scholar
Chen, W., Li, C., and Ou, B., Classification of solutions for an integral equation . Comm. Pure Appl. Math. 59(2006), 330–343.10.1002/cpa.20116CrossRefGoogle Scholar
Chen, W., Li, Y., and Ma, P., The fractional Laplacian, World Scientific Publishing Co. Pte. Ltd., Singapore, 2019.Google Scholar
Chen, W., Wang, P, Niu, Y. and Hu, Y., Asymptotic method of moving planes for fractional parabolic equations . Adv. Math. 377(2021), Article ID: 107463.10.1016/j.aim.2020.107463CrossRefGoogle Scholar
Chen, W. and Wu, L., The sliding methods for the fractional $p$ -Laplacian . Adv. Math. 361(2020), Article ID: 106933.Google Scholar
Chen, W. and Wu, L., Liouville theorems for fractional parabolic equations . Adv. Nonlinear Stud. 21(2021), no. 4, 939–958.10.1515/ans-2021-2148CrossRefGoogle Scholar
Chen, W. and Wu, L., Ancient solutions to nonlocal parabolic equations . Adv. Math. 408(2022), Article ID: 108607.Google Scholar
Chen, W. and Wu, L., Monotonicity and one-dimensional symmetry of solutions for fractional reaction-diffusion equations and various applications of sliding methods . Ann. di Mat. (2023). https://doi.org/10.1007/s10231-023-01357-4 CrossRefGoogle Scholar
Chen, W., Wu, L., and Wang, P, Nonexistence of solutions for indefinite fractional parabolic equations . Adv. Math. 392(2021), Article ID: 108018.10.1016/j.aim.2021.108018CrossRefGoogle Scholar
Chen, X. and Polác̆ik, P., Asymptotic periodicity of positive solutions of reaction diffusion equations on a ball . J. Reine Angew. Math. 472(1996), 17–52.Google Scholar
Chen, Y. and Liu, B., Symmetry and non-existence of positive solutions for fractional p-Laplacian systems . Nonlinear Anal. 183(2019), 303–322.10.1016/j.na.2019.02.023CrossRefGoogle Scholar
Constantin, P., Euler equations, Navier–Stokes equations and turbulence . In: Mathematical Foundation of Turbulent Viscous Flows, Lecture Notes in Mathematics, 1871, Springer, Berlin, 2006, pp. 1–43.Google Scholar
Dai, W., Peng, S., and Qin, G., Liouville type theorems, a priori estimates and existence of solutions for sub-critical order Lane–Emden–Hardy equations . J. Anal. Math. 146(2022), no. 2, 673–718.10.1007/s11854-022-0207-6CrossRefGoogle Scholar
Dai, W. and Qin, G., Classification of nonnegative classical solutions to third-order equations . Adv. Math. 328(2018), 822–857.10.1016/j.aim.2018.02.016CrossRefGoogle Scholar
Dai, W. and Qin, G., Maximum principles and the method of moving planes for the uniformly elliptic nonlocal Bellman operator and applications . Ann. Mat. Pura Appl. (4) 200(2021), no. 3, 1085–1134.10.1007/s10231-020-01027-9CrossRefGoogle Scholar
Dai, W., Qin, G., and Wu, D., Direct methods for pseudo-relativistic Schrödinger operators . J. Geom. Anal. 31(2021), no. 6, 5555–5618.10.1007/s12220-020-00492-1CrossRefGoogle Scholar
Deng, W., Li, B., Tian, W., and Zhang, P., Boundary problems for the fractional and tempered fractional operators . Multiscale Model. Simul. 16(2018), 125–149.10.1137/17M1116222CrossRefGoogle Scholar
Dipierro, S., Soave, N., and Valdinoci, E., On fractional elliptic equations in Lipschitz sets and epigraphs: Regularity, monotonicity and rigidity results . Math. Ann. 369(2017), 1283–1326.10.1007/s00208-016-1487-xCrossRefGoogle Scholar
Duo, S. and Zhang, Y., Numerical approximations for the tempered fractional Laplacian: Error analysis and applications . J. Sci. Comput. 81(2019), 569–593.10.1007/s10915-019-01029-7CrossRefGoogle Scholar
Frank, R. L., Lenzmann, E., and Silvestre, L., Uniqueness of radial solutions for the fractional Laplacian . Comm. Pure Appl. Math. 69(2013), no. 9, 1671–1726.10.1002/cpa.21591CrossRefGoogle Scholar
Guo, Y. and Peng, S., Symmetry and monotonicity of nonnegative solutions to pseudo-relativistic Choquard equations . Z. Angew. Math. Phys. 72(2021), no. 3, Article ID: 120.10.1007/s00033-021-01551-5CrossRefGoogle Scholar
Guo, Y. and Peng, S., Classification of solutions to mixed order conformally invariant systems in ${\mathbb{R}}^2$ . J. Geom. Anal. 32(2022), 178.10.1007/s12220-022-00916-0CrossRefGoogle Scholar
Guo, Y. and Peng, S., Maximum principles and direct methods for tempered fractional operators. To appear in Israel J. Math. (2022), 34pp.Google Scholar
Guo, Y. and Peng, S., Liouville-type results for positive solutions of pseudo-relativistic Schrödinger system . Proc. Roy. Soc. Edinburgh Sect. A. 153(2023), no. 1, 196–228.10.1017/prm.2021.81CrossRefGoogle Scholar
Guo, Y. and Peng, S., Liouville-type theorems for higher-order Lane–Emden system in exterior domains. Commun. Contemp. Math. 25(2023), no. 5, Article ID: 2250006.10.1142/S0219199722500067CrossRefGoogle Scholar
Hess, P., Poláčik, P., Symmetry and convergence properties for nonnegative solutions of nonautonomous reaction-diffusion problems . Proc. R. Soc. Edinb. Sect. A. 124(1994), 573–587.10.1017/S030821050002878XCrossRefGoogle Scholar
Li, C., Some qualitative properties of fully nonlinear elliptic and parabolic equations. Ph.D. thesis, New York University, 1989.Google Scholar
Li, C., Deng, W., and Zhao, L., Well-posedness and numerical algorithm for the tempered fractional ordinary differential equations . Discrete Contin. Dyn. Syst. Ser. B. 24(2019), 1989–2015.Google Scholar
Li, Y. Y., Remark on some conformally invariant integral equations: The method of moving spheres . J. Eur. Math. Soc. 6(2004), 153–180.10.4171/JEMS/6CrossRefGoogle Scholar
Peng, S., Existence and Liouville theorems for coupled fractional elliptic system with Stein–Weiss type convolution parts . Math. Z. 302(2022), no. 3, 1593–1626.10.1007/s00209-022-03130-4CrossRefGoogle Scholar
Peng, S., Classification of solutions to mixed order elliptic system with general nonlinearity . SIAM J. Math. Anal. 55(2023), no. 4, 2774–2812.10.1137/22M1510510CrossRefGoogle Scholar
Poláčik, P., Symmetry properties of positive solutions of parabolic equations on ${\mathbb{R}}^N$ , I: Asymptotic symmetry for the Cauchy problem . Commun. Partial Differ. Equ. 30(2005), 1567–1593.10.1080/03605300500299919CrossRefGoogle Scholar
Poláčik, P., Estimates of solutions and asymptotic symmetry for parabolic equations on bounded domains . Arch. Ration. Mech. Anal. 183(2007), 59–91.10.1007/s00205-006-0004-xCrossRefGoogle Scholar
Shiri, B., Wu, G., and Baleanu, D., Collocation methods for terminal value problems of tempered fractional differential equations . Appl. Numer. Math. 156(2020), 385–395.10.1016/j.apnum.2020.05.007CrossRefGoogle Scholar
Silvestre, L., Regularity of the obstacle problem for a fractional power of the Laplace operator . Comm. Pure Appl. Math. 60(2007), 67–112.10.1002/cpa.20153CrossRefGoogle Scholar
Wei, J. and Xu, X., Classification of solutions of higher order conformally invariant equations . Math. Ann. 313(1999), no. 2, 207–228.10.1007/s002080050258CrossRefGoogle Scholar
Zhang, L., Hou, W., Ahmad, B., and Wang, G., Radial symmetry for logarithmic Choquard equation involving a generalized tempered fractional p-Laplacian. Discrete Contin. Dyn. Syst. Ser. S 14(2021), no. 10, 3851–3863.Google Scholar
Zhang, Z., Deng, W., and Fan, H., Finite difference schemes for the tempered fractional Laplacian . Numer. Math. Theory Methods Appl. 12(2019), 492–516.10.4208/nmtma.OA-2017-0141CrossRefGoogle Scholar
Zhang, Z., Deng, W., and Karniadakis, G. E., A Riesz basis Galerkin method for the tempered fractional Laplacian . SIAM J. Numer. Anal. 56(2018), 3010–3039.10.1137/17M1151791CrossRefGoogle Scholar