Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-14T07:25:30.238Z Has data issue: false hasContentIssue false
  • English
  • Français

Singular Moduli of Shimura Curves

Published online by Cambridge University Press:  20 November 2018

Eric Errthum
Eric Errthum*
Affiliation:
Department of Mathematics & Statistics, Winona State University, Winona, MN, USA 55987 email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The 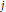$j$-function acts as a parametrization of the classical modular curve. Its values at complex multiplication (CM) points are called singular moduli and are algebraic integers. A Shimura curve is a generalization of the modular curve and, if the Shimura curve has genus 0, a rational parameterizing function exists and when evaluated at a CM point is again algebraic over $\mathbf{Q}$. This paper shows that the coordinate maps given by N. Elkies for the Shimura curves associated to the quaternion algebras with discriminants 6 and 10 are Borcherds lifts of vector-valued modular forms. This property is then used to explicitly compute the rational norms of singular moduli on these curves. This method not only verifies conjectural values for the rational CM points, but also provides a way of algebraically calculating the norms of CM points with arbitrarily large negative discriminant.

Keywords

11G1811F12
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 63 , Issue 4 , 01 August 2011 , pp. 826 - 861
Copyright
Copyright © Canadian Mathematical Society 2011

References

[1] Alsina, M. and Bayer, P., Quaternion orders, quadratic forms, and Shimura curves. CRM Monograph Series 22, American Mathematical Society, Providence, RI, 2004.Google Scholar
[2] Baba, S. and Granath, H., Genus 2 curves with quaternionic multiplication. Canad. J. Math. 60(2008), 734–757. doi:10.4153/CJM-2008-033-7Google Scholar
[3] Barnard, A., The Singular Theta Correspondence, Lorentzian Lattices and Borcherds–Kac–Moody Algebras. PhD Thesis, University of California, Berkeley, 2003.Google Scholar
[4] Borcherds, R., Automorphic forms with singularities on Grassmannians. Invent. Math. 132(1998), 491–562. doi:10.1007/s002220050232Google Scholar
[5] Borcherds, R., Reflection groups of Lorentzian lattices. Duke Math. J. 104(2000), 319–366. doi:10.1215/S0012-7094-00-10424-3Google Scholar
[6] Cremona, J. E., Algorithms for modular elliptic curves. Cambridge University Press, Cambridge, 1992.Google Scholar
[7] Elkies, N., Shimura curve computations. Algorithmic number theory (Portland, OR, 1998), Lecture Notes in Comput. Sci. 1423, Springer, Berlin, 1998, 1–47.Google Scholar
[8] Gross, B. and Zagier, D., On singular moduli. J. Reine Angew. Math. 355(1985), 191–220.Google Scholar
[9] Johansson, S., On fundamental domains of arithmetic Fuchsian groups. Math. Comp. 69(2000), 339–349. doi:10.1090/S0025-5718-99-01167-9Google Scholar
[10] Kudla, S. S., Integrals of Borcherds forms. Compositio Math. 137(2003), 293–349. doi:10.1023/A:1024127100993Google Scholar
[11] Kudla, S. S., Special cycles and derivatives of Eisenstein series. In: Heegner points and Rankin L-series, Math. Sci. Res. Inst. Publ. 49, Cambridge Univ. Press, Cambridge, 2004, 243–270.Google Scholar
[12] Kudla, S. S., Rapoport, M. and Yang, T., On the derivative of an Eisenstein series of weight one. Internat. Math. Res. Notices 1999(1999), 347–385. doi:10.1155/S1073792899000185Google Scholar
[13] Kudla, S. S., Modular forms and special cycles on Shimura curves. Ann. of Math. Stud. 161, Princeton University Press, Princeton, NJ, 2006.Google Scholar
[14] Kudla, S. S. and Yang, T., Eisenstein series for SL(2). Sci. China Math. 53(2010), no. 9, 2275–2316. doi:10.1007/s11425-010-4097-1Google Scholar
[15] Schofer, J., Borcherds forms and generalizations of singular moduli. J. Reine Angew. Math. 629(2009), 1–36. doi:10.1515/CRELLE.2009.025Google Scholar
[16] Vignéras, M.-F., Arithmétique des algèbres de quaternions. Lecture Notes in Mathematics 800, Springer, Berlin, 1980.Google Scholar