Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Jiang, Chunlan
Guo, Xianzhou
and
Ji, Kui
2005.
K-group and similarity classification of operators.
Journal of Functional Analysis,
Vol. 225,
Issue. 1,
p.
167.
Zhang, Zilong
and
Li, Yucheng
2006.
Algebra matrix and similarity classification of operators.
Science in China Series A,
Vol. 49,
Issue. 3,
p.
398.
Cao, Guang-fu
and
Wang, Xiao-hong
2007.
K-groups of Toeplitz algebras on connected domains.
Science in China Series A: Mathematics,
Vol. 50,
Issue. 1,
p.
73.
Jiang, Chun Lan
Jin, Yong Fei
and
Wang, Zong Yao
2007.
About Operator Weighted Shift.
Acta Mathematica Sinica, English Series,
Vol. 23,
Issue. 8,
p.
1385.
Jiang, Chun-lan
and
Li, Yu-cheng
2007.
The commutant and similarity invariant of analytic Toeplitz operators on Bergman space.
Science in China Series A: Mathematics,
Vol. 50,
Issue. 5,
p.
651.
Jung, Il Bong
and
Stochel, Jan
2008.
Subnormal operators whose adjoints have rich point spectrum.
Journal of Functional Analysis,
Vol. 255,
Issue. 7,
p.
1797.
Li, Yu Cheng
2008.
The commutant of analytic Toeplitz operators on Bergman space.
Acta Mathematica Sinica, English Series,
Vol. 24,
Issue. 10,
p.
1737.
He, Hua
Shi, Rui
and
Ma, XiuJuan
2008.
K 0-group and approximate similarity invariants of strongly irreducible operators.
Science in China Series A: Mathematics,
Vol. 51,
Issue. 12,
p.
2231.
Jiang, Chunlan
and
Zheng, Dechao
2010.
Similarity of analytic Toeplitz operators on the Bergman spaces.
Journal of Functional Analysis,
Vol. 258,
Issue. 9,
p.
2961.
Li, Jue-Xian
2011.
On commutativity of the commutant of strongly irreducible operator.
Proceedings of the American Mathematical Society,
Vol. 140,
Issue. 1,
p.
167.
Ji, Kui
2011.
Similarity Classification and Properties of Some Extended Holomorphic Curves.
Integral Equations and Operator Theory,
Vol. 69,
Issue. 1,
p.
133.
JIANG, CHUNLAN
2011.
A CLASSIFICATION OF NON-SIMPLE C*-ALGEBRAS OF TRACIAL RANK ONE: INDUCTIVE LIMITS OF FINITE DIRECT SUMS OF SIMPLE TAI C*-ALGEBRAS.
Journal of Topology and Analysis,
Vol. 03,
Issue. 03,
p.
385.
Zhang, Yunnan
and
Zhong, Huaijie
2011.
Strongly irreducible operators and Cowen-Douglas operators on c 0, l p (1 ⩽ p < ∞).
Frontiers of Mathematics in China,
Vol. 6,
Issue. 5,
p.
987.
Li, JueXian
2012.
K 0-group and similarity of operator weighted shifts.
Science China Mathematics,
Vol. 55,
Issue. 7,
p.
1441.
Ji, Kui
and
Shi, Rui
2013.
Similarity of multiplication operators on the Sobolev disk algebra.
Acta Mathematica Sinica, English Series,
Vol. 29,
Issue. 4,
p.
789.
JI, KUI
2014.
On a generalization of B 1 (Ω) on C ∗ -algebras.
Proceedings - Mathematical Sciences,
Vol. 124,
Issue. 2,
p.
243.
Dai, Hong
Hou, Yingli
and
Ji, Kui
2016.
A note on curvature and similarity of some Cowen–Douglas operators.
Journal of Mathematical Analysis and Applications,
Vol. 444,
Issue. 1,
p.
167.
Tian, Liang
Guo, Wei
and
Ji, Kui
2019.
A Note on a Subclass of Cowen-Douglas Operators.
Acta Mathematica Sinica, English Series,
Vol. 35,
Issue. 11,
p.
1795.
Ji, Kui
2019.
Curvature Formulas of Holomorphic Curves on
$$C^*$$
C
∗
-Algebras and Cowen–Douglas Operators.
Complex Analysis and Operator Theory,
Vol. 13,
Issue. 4,
p.
1609.
Jiang, Chunlan
and
Ji, Kui
2020.
Operator Theory, Operator Algebras and Their Interactions with Geometry and Topology.
Vol. 278,
Issue. ,
p.
373.
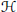 $\mathcal{H}$ be a complex separable Hilbert space and
$\mathcal{H}$ be a complex separable Hilbert space and 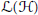 $\mathcal{L}\left( \mathcal{H} \right)$ denote the collection of bounded linear operators on
$\mathcal{L}\left( \mathcal{H} \right)$ denote the collection of bounded linear operators on 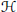 $\mathcal{H}$. An operator
$\mathcal{H}$. An operator 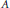 $A$ in
$A$ in 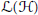 $\mathcal{L}\left( \mathcal{H} \right)$ is said to be strongly irreducible, if
$\mathcal{L}\left( \mathcal{H} \right)$ is said to be strongly irreducible, if 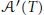 ${{\mathcal{A}}^{\prime }}(T)$, the commutant of
${{\mathcal{A}}^{\prime }}(T)$, the commutant of 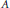 $A$, has no non-trivial idempotent. An operator
$A$, has no non-trivial idempotent. An operator 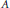 $A$ in
$A$ in 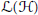 $\mathcal{L}\left( \mathcal{H} \right)$ is said to be a Cowen-Douglas operator, if there exists
$\mathcal{L}\left( \mathcal{H} \right)$ is said to be a Cowen-Douglas operator, if there exists 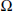 $\Omega $, a connected open subset of
$\Omega $, a connected open subset of 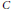 $C$, and
$C$, and  $n$, a positive integer, such that
$n$, a positive integer, such that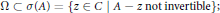 $$\Omega \,\subset \,\sigma (A)\,=\,\left\{ z\,\in \,C|\,A-z\,\text{not}\,\text{invertible} \right\};$$
$$\Omega \,\subset \,\sigma (A)\,=\,\left\{ z\,\in \,C|\,A-z\,\text{not}\,\text{invertible} \right\};$$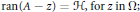 $$\text{ran(A}-z\text{)}\,\text{=}\,\mathcal{H}\text{,}\,\text{for}\,z\,\text{in}\,\Omega \text{;}$$
$$\text{ran(A}-z\text{)}\,\text{=}\,\mathcal{H}\text{,}\,\text{for}\,z\,\text{in}\,\Omega \text{;}$$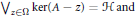 $${{\vee }_{z\in \Omega }}\,\ker (A-\,z)\,=\,\mathcal{H}\,\text{and}$$
$${{\vee }_{z\in \Omega }}\,\ker (A-\,z)\,=\,\mathcal{H}\,\text{and}$$ $$\dim\,\ker (A-z)\,=\,n\,\text{for}\,z\,\text{in}\,\Omega $$
$$\dim\,\ker (A-z)\,=\,n\,\text{for}\,z\,\text{in}\,\Omega $$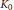 ${{K}_{0}}$-group of the commutant algebra as an invariant.
${{K}_{0}}$-group of the commutant algebra as an invariant.

