Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-12-02T23:31:00.216Z Has data issue: false hasContentIssue false
  • English
  • Français

Sharply Transferable Lattices

Published online by Cambridge University Press:  20 November 2018

H. Gaskill ,
G. Grätzer  and
C. R. Platt
H. Gaskill
Affiliation:
The University of Manitoba, Winnipeg, Manitoba
G. Grätzer
Affiliation:
The University of Manitoba, Winnipeg, Manitoba
C. R. Platt
Affiliation:
The University of Manitoba, Winnipeg, Manitoba
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In a lecture in 1966 (see [6]), the second author considered briefly those first order properties which hold for a lattice 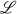if and only if they hold for the lattice 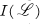of all ideals of 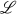. The best known examples of such properties are those given by identities. The well-known connection between the modular identity ϵ and the five-element nonmodular lattice 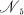transforms the above result for ϵ into the following statement: 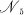is a sublattice of a lattice 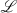if and only if 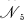is a sublattice of .

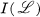Type
Research Article
Information
Canadian Journal of Mathematics , Volume 27 , Issue 6 , 01 December 1975 , pp. 1246 - 1262
Copyright
Copyright © Canadian Mathematical Society 1975

References

1. Baker, K. and Hales, A., From a lattice to its ideal lattice, Algebra Universalis 4 (1974), 250–258.Google Scholar
2. Day, A., A simple solution of the word problem for lattices, Can. Math. Bull. 13 (1970), 253–254.Google Scholar
3. Gaskill, H., On transferable semilattices, Algebra Universalis 2 (1973), 303–316.Google Scholar
4. Gaskill, H., Transferability in lattices and semilattices, Ph.D. Thesis, Simon Fraser University, 1972.Google Scholar
5. Gaskill, H. and Piatt, C. R., Sharp transferability andfinite sublattices of free lattices, to appearGoogle Scholar
6. Gràtzer, G., Universal algebra in Trends in lattice theory (Abbot, J. C., Editor, pp. 173–215. New York, Van Nostrand Reinhold 1970).Google Scholar
7. Gràtzer, G., Lattice theory : First concepts and distributive lattices (San Francisco, W. H. Freeman 1971).Google Scholar
8. Gràtzer, G., General lattice theory (Academic Press, forthcoming).Google Scholar
9. Gràtzer, G., A property of transferable lattices, Proc. Amer. Math. Soc, to appear.Google Scholar
10. Jônsson, B., Sublattices of a free lattice, Can. J. Math. 13 (1961), 256–264.Google Scholar
11. Jônsson, B. and Kiefer, J., Finite sublattices of a free lattice, Can. J. Math. 14 (1962), 487–497.Google Scholar
12. McKenzie, R., Equational bases and nonmodular lattice varieties, Trans. Amer. Math. Soc. 174 (1972), 1–43.Google Scholar
13. Whitman, P. M., Free lattices I and II, Annals of Math. 42 (1941), 325-330 and 43 (1942), 104–115.Google Scholar