Article contents
Shape Equivalences of Whitney Continua of Curves
Published online by Cambridge University Press: 20 November 2018
Extract
By a compactum, we mean a compact metric space. A continuum is a connected compactum. A curve is a 1-dimensional continuum. Let X be a continuum and let C(X) be the hyperspace of (nonempty) subcontinua of X, C(X) is metrized with the Hausdorff metric (e.g., see [12] or [18]). One of the most convenient tools in order to study the structure of C(X) is a monotone map ω:C(X) → [0, ω(X)] defined by H. Whitney [25]. A map ω:C(X) → [0, ω(X)] is said to be a Whitney map for C(X) provided that
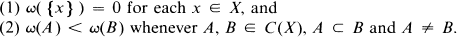
The continua {ω−1} (0 < t < ω(X)) are called the Whitney continua of X. We may think of the map ω as measuring the size of a continuum. Note that ω−1(0) is homeomorphic to X and ω−1(ω(X)) = {X}. Naturally, we are interested in the structures of ω−1(t)(0 < t < ω(X)). In [14], J. Krasinkiewicz proved that if X is a circle-like continuum and ω is any Whitney map for C(X), then for any 0 < t < ω(X)ω−1(t) is shape equivalent to X, i.e., Sh ω−1(t) = Sh X (e.g., see [1] or [17]). In [8], we proved the following: If one of the conditions (i) and (ii) is satisfied, then the shape morphism
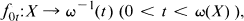
which is defined in [7] and [8], is a shape equivalence.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1988
References
- 4
- Cited by


