Hostname: page-component-745bb68f8f-mzp66 Total loading time: 0 Render date: 2025-02-03T01:39:28.706Z Has data issue: false hasContentIssue false
  • English
  • Français

Sets of Uniqueness for the Group of Integers of a p-Series Field

Published online by Cambridge University Press:  20 November 2018

William R. Wade
William R. Wade*
Affiliation:
The University of Tennessee, Knoxville, Tennessee
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let G denote the group of integers of a p-series field, where p is a prime ≦ 2. Thus, any element 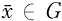can be represented as a sequence {xi }i = 0∞ with 0 ≦ xi < p for each i ≦ 0. Moreover, the dual group {Ψm}m = 0∞ of G can be described by the following process. If m is a non-negative integer with 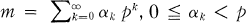for each k , and if 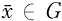then

(1)

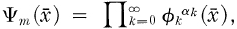
where for each integer k ≧ 0 and for each x = {xi} ∈ G the functions Φk are defined by

(2)

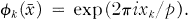
In the case that p = 2, the group G is the dyadic group introduced by Fine [1] and the functions 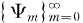are the Walsh-Paley functions. A detailed account of these groups and basic properties can be found in [4].

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 31 , Issue 4 , 01 August 1979 , pp. 858 - 866
Copyright
Copyright © Canadian Mathematical Society 1979

References

1. Fine, N. J., On the Walsh functions, Trans, A. M. S. 65 (1949), 372–414.Google Scholar
2. Lindahl, R. J., A differentiation theorem for functions defined on the dyadic rationals, Proc. A. M. S. 30 (1971), 349–352.Google Scholar
3. Sneider, A., On uniqueness of expansions in Walsh functions, Mat. Sbornik N. S. 24 (1949), 379–400.Google Scholar
4. Taibleson, M. H., Fourier analysis on local fields (Mathematical Notes, Princeton University Press, Princeton, 1975).Google Scholar
5. Wade, W. R., Uniqueness and a-capacity on the group 2”, Trans. A. M. S. 208 (1975), 309–315.Google Scholar
6. Zygmund, A., Trigonometric series (2nd ed. Vol. I, Cambridge University Press, New York, 1959).Google Scholar