Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-25T05:18:56.809Z Has data issue: false hasContentIssue false
  • English
  • Français

A Set of Plane Measure Zero Containing all Finite Polygonal Arcs

Published online by Cambridge University Press:  20 November 2018

D. J. Ward
D. J. Ward*
Affiliation:
The University of Toronto, Toronto, Ontario The University of Sussex, Brighton, England
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We say a (plane) set A contains all sets of some type 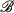if, for each B of type 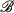, there is a subset of A that is congruent to B. Recently, Besicovitch and Rado [3] and independently, Kinney [5] have constructed sets of plane measure zero containing all circles. In these papers it is pointed out that the set of all similar rectangles, some sets of confocal conies and other such classes of sets can be contained in sets of plane measure zero, but all these generalizations rely in some way on the symmetry, or similarity of the sets within the given type.

In this paper we construct a set of plane measure zero containing all finite polygonal arcs (i.e., the one-dimensional boundaries of all polygons with a finite number of sides) with slightly stronger results if we restrict our attention to k-gons for some fixed k.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 22 , Issue 4 , 01 August 1970 , pp. 815 - 821
Copyright
Copyright © Canadian Mathematical Society 1970

References

1. Besicovitch, A. S., On linear sets of points of fractional dimension, Math. Ann. 101 (1929), 161–193.Google Scholar
2. Besicovitch, A. S. and Moran, P. A. P., The measure of product and cylinder sets, J. London Math. Soc. 20 (1945), 110–120.Google Scholar
3. Besicovitch, A. S. and Rado, R., A plane set of measure zero containing circumferences of every radius, J. London Math. Soc. 43 (1968), 717–719.Google Scholar
4. Davies, R. O., Marstrand, J. M., and Taylor, S. J., On the intersections of transforms of linear sets, Colloq. Math. 7 (1959/60), 237–243.Google Scholar
5. Kinney, J. R., A thin set of circles, Amer. Math. Monthly 75 (1968), 1077–1081.Google Scholar