Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-27T22:41:08.820Z Has data issue: false hasContentIssue false
  • English
  • Français

Separating Points of βℕ By Minimal Flows

Published online by Cambridge University Press:  20 November 2018

Neil Hindman ,
Jimmie Lawson  and
Amha Lisan
Neil Hindman
Affiliation:
Department of Mathematics, Howard University Washington, D. C. 20059, U.S.A.
Jimmie Lawson
Affiliation:
Department of Mathematics, Louisiana State University Baton Rouge, Louisiana 70803, U.S.A.
Amha Lisan
Affiliation:
Department of Mathematics, Louisiana State University Baton Rouge, Louisiana 70803, U.S.A.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider minimal left ideals L of the universal semigroup compactification 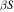of a topological semigroup S. We show that the enveloping semigroup of L is homeomorphically isomorphic to 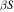if and only if given q ≠ r in 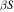, there is some p in the smallest ideal of 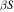with qp ≠ rp. We derive several conditions, some involving minimal flows, which are equivalent to the ability to separate q and r in this fashion, and then specialize to the case that S = , and the compactification is 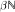. Included is the statement that some set A whose characteristic function is uniformly recurrent has .

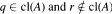Keywords

22A30
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 46 , Issue 4 , 01 August 1994 , pp. 758 - 771
Copyright
Copyright © Canadian Mathematical Society 1994

References

1. Baker, J. and Milnes, P., The ideal structure of the Stone-Cech compactification of a group, Math. Proc. Cambridge Philos. Soc. 82(1977), 401–409.Google Scholar
2. Berglund, J. and Hindman, N., Sums of idempotents in , Semigroup Forum 44(1992), 107–111.Google Scholar
3. Berglund, J., Junghenn, H. and Milnes, P., Analysis on Semigroups, Wiley, New York, 1989.Google Scholar
4. Ellis, R., A semigroup associated with a transformation group, Trans. Amer. Math. Soc. 94( 1960), 272–281.Google Scholar
5. Ellis, R., Lectures on Topological Dynamics, Benjamin, New York, 1969.Google Scholar
6. Furstenberg, H., Recurrence in Ergodic Theory and Combinatorial Number Theory, Princeton Univ. Press, Princeton, 1981.Google Scholar
7. Gottschalk, W., Almost periodic points with respect to transformation semi-groups, Ann. of Math. 47(1946), 762–766.Google Scholar
8. Hindman, N., Minimal ideals and cancellation in , Semigroup Forum 25(1982), 291–310.Google Scholar
9. Hindman, N., Sums equal to products in , Semigroup Forum 21(1980), 221–255.Google Scholar
10. Hindman, N., Ultrafilters and combinatorial number theory. In: Number Theory Carbondale, Springer Lecture Notes in Math. (ed. M. Nathanson),751, 1979, 119–184.Google Scholar
11. Lawson, J. and A. Lisan, Transitive flows: a semigroup approach, Mathematika 38(1991), 348–361.Google Scholar
12. Ruppert, W., Compact semitopological semigroups: an intrinsic theory, Lecture Notes in Math. 1079, Springer, 1984.Google Scholar
13. Ruppert, W., Endomorphic actions of on the torus group, Semigroup Forum 43(1991), 202–217.Google Scholar
14. Strauss, D., Ideals and commutativity in , Topology Appl., to appear.Google Scholar