Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-25T06:12:56.041Z Has data issue: false hasContentIssue false
  • English
  • Français

Separating Closed Sets by Continuous Mappings into Developable Spaces

Published online by Cambridge University Press:  20 November 2018

Harald Brandenburg
Harald Brandenburg*
Affiliation:
Freie Universität Berlin, Berlin, Federal Republic of Germany
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A topological space X is called developable if it has a development, i.e., a sequence 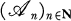of open covers of X such that for each x ∈ X the collection 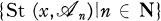is a neighbourhood base of x, where

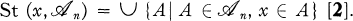
This class of spaces has turned out to be one of the most natural and useful generalizations of metrizable spaces [23]. In [4] it was shown that some well known results in metrization theory have counterparts in the theory of developable spaces (i.e., Urysohn's metrization theorem, the Nagata-Smirnov theorem, and Nagata's “double sequence theorem”). Moreover, in [3] it was pointed out that subspaces of products of developable spaces (i.e., D-completely regular spaces) can be characterized in much the same way as subspaces of products of metrizable spaces (i.e., completely regular T1-spaces).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 33 , Issue 6 , 01 December 1981 , pp. 1420 - 1431
Copyright
Copyright © Canadian Mathematical Society 1981

References

1. Alster, K. and Engelking, R., Subparacompactness and product spaces, Bull. Acad. Polon. Sci. 20 (1972), 763–767.Google Scholar
2. Bing, R. H., Metrization of topological spaces, Can. J. Math. 3 (1951), 175–186.Google Scholar
3. Brandenburg, H., On a class of nearness spaces and the epireflective hull of developable topological spaces, in: Proceedings of the International Symposium on Topology and its Appl. (Beograd, 1977), (to appear).Google Scholar
4. Brandenburg, H., Some characterizations of developable spaces, Proc. Amer. Math. Soc. 80 (1980), 157–161.Google Scholar
5. Brandenburg, H., On spaces with a Gδ-basis, Arch. Math. 35 (1980), 544–547.Google Scholar
6. Brandenburg, H., A characterization of perfect spaces, unpublished manuscript.Google Scholar
7. Chaber, J., Conditions which imply compactness in countably compact spaces, Bull. Acad. Polon. Sci. 24 (1976), 993–998.Google Scholar
8. Chaber, J., On subparacompactness and related properties, General Topol. Appl. 10 (1979), 13–17.Google Scholar
9. Heath, R. W. and Michael, E. A., A property of the Sorgenfrey line, Compositio Math. 23 (1971), 185–188.Google Scholar
10. Heldermann, N. C., The category of D-completely regular spaces is simple, Trans. Amer. Math. Soc. 262 (1980), 437–446.Google Scholar
11. Heldermann, N. C., Developability and some new regularity axioms, Can. J. Math. 33 (1981), 641–663.Google Scholar
12. Herrlich, H., A concept of nearness, General Topol. Appl. 5 (1974), 191–212.Google Scholar
13. Inokuma, T., On a characteristic property of completely normal spaces, Proc. Japan Acad. 31 (1955), 56–59.Google Scholar
14. Isbell, J. R., A note on complete closure algebras, Math. Systems Theory 3 (1969), 310–312.Google Scholar
15. Katětov, M., Complete normality of cartesian products, Fund. Math. 35 (1948), 271–274.Google Scholar
16. Misra, A. K., A topological view of P-spaces, General Topol. Appl. 2 (1972), 349–362.Google Scholar
17. Mysior, A., Two remarks on D-regular spaces, Glasnik Mat., III. Ser. 15, 35 (1980), 153–156.Google Scholar
18. Pareek, C. M., Moore spaces, semi-metric spaces and continuous mappings connected with them, Can. J. Math. 24 (1972), 1033–1042.Google Scholar
19. Pears, A. R., Dimension theory of general spaces, (Cambridge University Press, Cambridge et al., 1975).Google Scholar
20. Smirnov, Yu. M., On normally placed sets in normal spaces, Mat. Sbornik 29 (1951), 173–176, (in Russian).Google Scholar
21. Steen, L. A. and Seebach, J. A., Jr., Counterexamples in topology, (Springer Verlag, Berlin et al., 1978).Google Scholar
22. Tukey, J. W., Convergence and uniformity in topology, Ann. of Math. Studies 2 (Princeton, 1940).Google Scholar
23. Worrell, J. M., Jr. and Wicke, H. H., Characterizations of developable topological spaces, Can. J. Math. 17 (1965), 820–830.Google Scholar
24. Worrell, J. M., Jr., Upper semicontinuous decompositions of developable spaces, Proc. Amer. Math. Soc. 16 (1965), 485–490.Google Scholar