Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-18T13:08:59.636Z Has data issue: false hasContentIssue false
  • English
  • Français

A Semilinear Problem for the Heisenberg Laplacian on Unbounded Domains

Published online by Cambridge University Press:  20 November 2018

Sara Maad
Sara Maad*
Affiliation:
Department of Mathematics and Statistics, School of Electronic and Physical Sciences, University of Surrey, Guildford, Surrey, GUZ 7XH, U.K., e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the semilinear equation

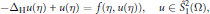$$-{{\Delta }_{\mathbb{H}}}u(\eta )\,+\,u(\eta )\,=\,f(\eta ,\,\,u(\eta )),\,u\in \,\overset{\circ }{\mathop{S}}\,_{1}^{2}(\Omega ),$$

where 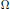$\Omega $ is an unbounded domain of the Heisenberg group ${{\mathbb{H}}^{N}},\,N\,\ge \,1$. The space 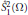$\overset{\circ }{\mathop{S}}\,_{1}^{2}(\Omega )$ is the Heisenberg analogue of the Sobolev space 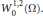$W_{0}^{1,\,2}\,\left( \Omega \right)$. The function 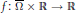$f\,:\,\overset{-}{\mathop{\Omega }}\,\,\times \,\mathbb{R}\,\to \,\mathbb{R}$ is supposed to be odd in 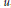$u$, continuous and satisfy some (superlinear but subcritical) growth conditions. The operator 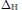${{\Delta }_{\mathbb{H}}}$ is the subelliptic Laplacian on the Heisenberg group. We give a condition on 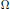$\Omega $ which implies the existence of infinitely many solutions of the above equation. In the proof we rewrite the equation as a variational problem, and show that the corresponding functional satisfies the Palais–Smale condition. This might be quite surprising since we deal with domains which are far frombounded. The technique we use rests on a compactness argument and the maximum principle.

Keywords

22E3022E27Heisenberg groupconcentration compactnessHeisenberg Laplacian
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 57 , Issue 6 , 01 December 2005 , pp. 1279 - 1290
Copyright
Copyright © Canadian Mathematical Society 2005

References

[1] Birindelli, I. and Cutrì, A., A semi-linear problem for the Heisenberg Laplacian. Rend. Sem. Mat. Univ. Padova 94(1995), 137–153.Google Scholar
[2] Bony, J. M., Principe du maximum, inégalité de Harnack et unicité du problème de Cauchy pour les opérateurs elliptiques dégénérés. Ann. Inst. Fourier (Grenoble) 19(1969), 277–304.Google Scholar
[3] del Pino, M. A. and Felmer, P. L., Least energy solutions for elliptic equations in unbounded domains. Proc. Roy. Soc. Edinburgh Sect. A 126(1996), 195–208.Google Scholar
[4] Folland, G. B. and Stein, E. M., Estimates for the ∂b complex and analysis on the Heisenberg group. Comm. Pure Appl. Math. 27(1974), 429–522.Google Scholar
[5] Garofalo, N. and Lanconelli, E., Existence and nonexistence results for semilinear equations on the Heisenberg group. Indiana Univ.Math. J. 41(1992), 71–98.Google Scholar
[6] Hörmander, L., Hypoelliptic second order differential equations. Acta math. 119(1967), 147–171.Google Scholar
[7] Maad, S., Multiplicity of solutions of nonlinear elliptic equations with Z/2-symmetry. U.U.D.M. Report 2001:12, ISSN 1101-3591, http://www.math.uu.se/research/pub/Maad1.pdfGoogle Scholar
[8] Maad, S., Infinitely many solutions of a symmetric semilinear equation on an unbounded domain. Ark.Mat. 41(2003), 105–114.Google Scholar
[9] Schindler, I. and Tintarev, K., An abstract version of the concentration compactness principle. Rev. Mat. Complut. 15(2002), 417–436.Google Scholar
[10] Struwe, M., Variational methods. Second Edition, Springer-Verlag, Berlin, 1996.Google Scholar
[11] Tintarev, K., Semilinear elliptic problems on unbounded subsets of the Heisenberg group. Electron. J. Differential Equations 2001, 18.Google Scholar
[12] Tintarev, K., Semilinear subelliptic problems without compactness on Lie groups. NoDEA Nonlinear Differential Equations Appl. 11(2004), 299–309.Google Scholar