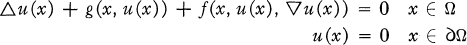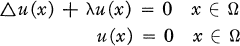Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Boccardo, Lucio
Dràbek, Pavel
Giachetti, Daniela
and
Kučera, Milan
1986.
Generalization of Fredholm alternative for nonlinear differential operators.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 10,
Issue. 10,
p.
1083.
Hai, D.D.
and
Schmitt, K.
1993.
Existence and Uniqueness Results for Nonlinear Boundary Value Problems.
Rocky Mountain Journal of Mathematics,
Vol. 24,
Issue. 1,