Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-08T07:30:09.422Z Has data issue: false hasContentIssue false
  • English
  • Français

Semi-Classical Behavior of the Scattering Amplitude for Trapping Perturbations at Fixed Energy

Published online by Cambridge University Press:  20 November 2018

Laurent Michel
Laurent Michel*
Affiliation:
Département de Mathématiques, Institut Galillee, Université Paris 13, 99, avenue J.-B. Clement France e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the semi-classical behavior as 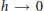$h\,\to \,0$ of the scattering amplitude 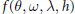$f(\theta ,\,\omega ,\,\lambda ,\,h)$ associated to a Schrödinger operator 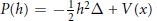$P(h)\,=\,-\,\frac{1}{2}{{h}^{2}}\Delta \,+\,V\,(x)$ with short-range trapping perturbations. First we realize a spatial localization in the general case and we deduce a bound of the scattering amplitude on the real line. Under an additional assumption on the resonances, we show that if we modify the potential 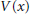$V(x)$ in a domain lying behind the barrier $\left\{ x\,:\,V(x)\,>\,\lambda \right\}$, the scattering amplitude 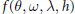$f(\theta ,\,\omega ,\,\lambda ,\,h)$ changes by a term of order 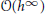$\mathcal{O}({{h}^{\infty }})$. Under an escape assumption on the classical trajectories incoming with fixed direction 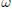$\omega $, we obtain an asymptotic development of 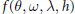$f(\theta ,\,\omega ,\,\lambda ,\,h)$ similar to the one established in the non-trapping case.

Keywords

35P2535B3435B40
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 56 , Issue 4 , 01 August 2004 , pp. 794 - 824
Copyright
Copyright © Canadian Mathematical Society 2004

References

[1] Bruneau, V. and Petkov, V., Semiclassical resolvent estimates for trapping perturbations. Comm. Math. Phys. 213(2000), 413–432.Google Scholar
[2] Burq, N., Lower bounds for shape resonances width of long range Schrödinger operators. Amer. J. Math. 124(2002), 677–735.Google Scholar
[3] Derezínski, J. and Gérard, C., Scattering theory of classical and quantum n-particle systems. Springer-Verlag, Berlin, 1997.Google Scholar
[4] Gérard, C., Asymptotique des pôles de la matrice de scattering pour deux obstacles strictement convexes. Mém. Soc. Math. France 31(1988).Google Scholar
[5] Gérard, C. and Sjöstrand, J., Semiclassical resonances generated by a closed trajectory of hyperbolic type. Comm. Math. Phys. 108(1987), 391–421.Google Scholar
[6] Hörmander, L., The analysis of linear partial differential operators I. Grundlehren Math. Wiss. 256(1983).Google Scholar
[7] Isozaki, H. and Kitada, H., Modified wave operators with time-independent modifiers. J. Fac. Sci. Univ. Tokyo, Sect. IA, Math. 32(1985), 77–104.Google Scholar
[8] Isozaki, H. and Kitada, H., Scattering matrices for two-body Schrödinger operators. Sci. Papers College Arts Sci. Univ. Tokyo, 35(1986), 81–107.Google Scholar
[9] Ivrii, V., Microlocal analysis and precise spectral asymptotics. Springer-Verlag, Berlin, 1998.Google Scholar
[10] Lahmar-Benbernou, A. and Martinez, A., Semiclassical asymptotics of the residues of the scattering matrix for shape resonances. Asympt. Anal. 20(1999), 13–38.Google Scholar
[11] Martinez, A., Resonance free domains for non-analytic potentials. Preprint, Univ. di Bologna, 2001.Google Scholar
[12] Maslov, V. P. and Fedoriuk, M. V., Semi-classical approximation in quantum mechanics. D. Reidel, Dordrecht, 1981.Google Scholar
[13] Michel, L., Semi-classical limit of the scattering amplitude for trapping perturbations. Asympt. Anal. 32(2002), 221–255.Google Scholar
[14] Michel, L., Asymptotiques semiclassiques de l’amplitude de diffusion pour des perturbations captives. Thèse Univ. Bordeaux I, 2002.Google Scholar
[15] Michel, L., Semi-classical estimate of the residue of the scattering amplitude for long-range potentials. J. Phys. A 36(2003), 4375–4393.Google Scholar
[16] Nakamura, S., Scattering theory for the shape resonance model i. non-resonant energies. Ann. Inst. H. Poincaré Phys. Théor. 50(1989), 115–131.Google Scholar
[17] Petkov, V. and Zworski, M., Semiclassical estimate of the scattering determinant. Ann. Henri Poincaré, 2(2001), 675–711.Google Scholar
[18] Reed, M. and Simon, B., Methods of modern mathematical physics III, Scattering theory. Academic Press, New York, 1979.Google Scholar
[19] Robert, D. and Tamura, H., Semiclassical estimates for resolvents and asymptotics for total scattering cross-sections. Ann. Inst. H. Poincaré Phys. Théor. 46(1987), 415–442.Google Scholar
[20] Robert, D. and Tamura, H., Asymptotic behavior of scattering amplitudes in semi-classical and low energy limits. Ann. Inst. Fourier (Grenoble) 39(1989), 155–192.Google Scholar
[21] Sjöstrand, J.. A trace formula and review of some estimates for resonances. NATO Adv. Sci. Inst. Ser. C 490(1997), 377–437.Google Scholar
[22] Sjöstrand, J. and Zworski, M., Complex scaling and the distribution of scattering poles. J. Amer.Math. Soc. 4(1991), 729–769.Google Scholar
[23] Stefanov, P., Estimates on the residue of the scattering amplitude. Asympt. Anal. 32(2002), 317–333.Google Scholar
[24] Tang, S. H. and Zworski, M., From quasi-modes to resonances. Math. Res. Lett. 5(1998), 261–272.Google Scholar
[25] Vainberg, B. R., Quasi-classical approximation in stationary scattering problems. Functional Anal. Appl. 11(1977), 247–257.Google Scholar
[26] Vainberg, B. R., Asymptotic methods in equations of mathematical physics. Gordon and Breach Science Publishers, New York, 1989.Google Scholar
[27] Yajima, K., The quasi-classical limit of scattering amplitude: L 2 approach for short range potentials. Japan. J. Math. 13(1987), 77–126.Google Scholar