Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Strade, H.
1994.
The classification of the simple modular lie algebras: V. algebras with Hamiltonian two-sections.
Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg,
Vol. 64,
Issue. 1,
p.
167.
Premet, Alexander
and
Strade, Helmut
1997.
Simple Lie Algebras of Small Characteristic: I. Sandwich Elements.
Journal of Algebra,
Vol. 189,
Issue. 2,
p.
419.
Premet, Alexander
and
Strade, Helmut
2004.
Simple Lie algebras of small characteristic IV..
Journal of Algebra,
Vol. 278,
Issue. 2,
p.
766.
Caranti, A.
and
Mattarei, S.
2005.
Gradings of non-graded Hamiltonian Lie algebras.
Journal of the Australian Mathematical Society,
Vol. 79,
Issue. 3,
p.
399.
Premet, Alexander
and
Strade, Helmut
2007.
Simple Lie algebras of small characteristic V. The non-Melikian case.
Journal of Algebra,
Vol. 314,
Issue. 2,
p.
664.


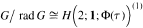 is an algebra mentioned in the title, the modules of dimension ≤
is an algebra mentioned in the title, the modules of dimension ≤ 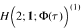 .
.