Hostname: page-component-5cf477f64f-2wr7h Total loading time: 0 Render date: 2025-04-05T01:58:15.084Z Has data issue: false hasContentIssue false
  • English
  • Français

A Remark on the Proof of a Theorem of Laufer and Tomber

Published online by Cambridge University Press:  20 November 2018

Hyo Chul Myung
Hyo Chul Myung*
Affiliation:
Michigan State University, East Lansing, Michigan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this note we give a correction to the proof of the following theorem [1, Theorem 2].

THEOREM. Let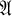be a flexible, power-associative algebra, over an arbitrary algebraically closed field Ω of characteristic 0. If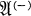is a simple Lie algebra, then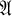is a simple Lie algebra isomorphic to.

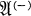Step (i) of the proof, which proves that the Cartan subalgebra 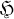of 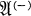is a nil subalgebra of 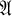, is incomplete. Assuming that 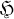is not a nil subalgebra of 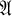, there exists an idempotent e ≠ 0 in .

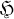Type
Research Article
Information
Canadian Journal of Mathematics , Volume 23 , Issue 2 , April 1971 , pp. 270
Copyright
Copyright © Canadian Mathematical Society 1971

References

1. Laufer, P. J. and Tomber, M. L., Some Lie admissible algebras, Can. J. Math. 14 (1962), 287–292.Google Scholar
2. Oehmke, R. H., On flexible algebras, Ann. of Math. (2) 68 (1958), 221–230.Google Scholar