Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-02T23:29:39.782Z Has data issue: false hasContentIssue false
  • English
  • Français

A Remark on Colimits

Published online by Cambridge University Press:  20 November 2018

Barbara L. Osofsky
Barbara L. Osofsky*
Affiliation:
Rutgers University, New Brunswick, New Jersey
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let MR be a right module over the associative ring R (with 1). Assume one has an expression for M as a colimit (direct limit) of a system

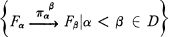
over the (directed) poset D. A natural way to get M as a colimit of the family ﹛F∞ —” Fβ|∞, fβ ∈ E﹜ for some subset £ of D is to take E cofinal in D. However, if one is concerned about the cardinality of the set E, cofinal subsets may be too large. Let us look at a specific example. Lazard [3] has shown that any flat MR is a direct limit of finitely generated free R-modules. The cardinality of his indexing set depends on the cardinality of M.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 27 , Issue 3 , 01 June 1975 , pp. 496 - 499
Copyright
Copyright © Canadian Mathematical Society 1975

References

1. Kaplansky, I., Projective modules, Ann. of Math. 68 (1958), 372–377.Google Scholar
2. Kaplansky, I., Fields and rings (University of Chicago Press, Chicago, 1969).Google Scholar
3. Lazard, D., Sur les modules plats, C. R. Acad Sci. Paris 258 (1964), 6313–6316.Google Scholar
4. Osofsky, B., Upper bounds on homologuai dimensions, Nagoya Math. J. 32 (1968), 315–322.Google Scholar
5. Osofsky, B., Homological dimensions of modules, Conference Board of the Mathematical Sciences Regional Conference Series in Mathematics, Number 12 (American Math. Soc, Providence, 1973). Google Scholar
6. Eilenberg, S. and Steenrod, N., Foundations of algebraic topology (Princeton University Press, Princeton, 1952).Google Scholar