Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-17T17:13:18.040Z Has data issue: false hasContentIssue false
  • English
  • Français

Relative Discrete Series Representations for Two Quotients of p-adic GLn

Published online by Cambridge University Press:  20 November 2018

Jerrod Manford Smith
Jerrod Manford Smith*
Affiliation:
Department of Mathematics, University of Toronto, Toronto, Canada, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We provide an explicit construction of representations in the discrete spectrum of two 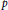$p$-adic symmetric spaces. We consider 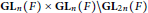$\text{G}{{\text{L}}_{n}}\left( F \right)\,\times \,\text{G}{{\text{L}}_{n}}\left( F \right)\backslash \text{G}{{\text{L}}_{2n}}\left( F \right)$ and 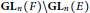$\text{G}{{\text{L}}_{n}}\left( F \right)\,\backslash \text{G}{{\text{L}}_{n}}\left( E \right)$, where $E$ is a quadratic Galois extension of a nonarchimedean local field $F$ of characteristic zero and odd residual characteristic. The proof of the main result involves an application of a symmetric space version of Casselman’s Criterion for square integrability due to Kato and Takano.

Keywords

22E5022E35p-adic symmetric spacerelative discrete seriesCasselman’s Criterion
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 70 , Issue 6 , 01 December 2018 , pp. 1339 - 1372
Copyright
Copyright © Canadian Mathematical Society 2018

References

[1] Anandavardhanan, U. K., Root numbers ofAsai L-functions. Int. Math. Res. Not. IMRN (2008), Art. ID rnnl25, 25.Google Scholar
[2] Anandavardhanan, U. K. and Rajan, C. S., Distinguished representations, base change, and reducibility for unitary groups. Int. Math. Res. Not. (2005), no. 14, 841-854.Google Scholar
[3] Bernstein, I. N. and Zelevinsky, A. V., Representations of the group GL( n, F), where F is a local non-Archimedean field. Uspehi Mat. Nauk 31 (1976), no. 3(189), 5–70.Google Scholar
[4] Bernstein, I. N. and Zelevinsky, A. V., Induced representations of reductive p-adic groups. I. Ann. Sci. École Norm. Sup. (4) 10 (1977), no. 4, 441–472. http://dx.doi.Org/10.24033/asens.1333Google Scholar
[5] Bruhat, François, Distributions sur un groupe localement compact et applications à l'étude des représentations des groupes p-adiques. Bull. Soc. Math. France 89 (1961), 43–75. http://dx.doi.Org/10.24033/bsmf.1559Google Scholar
[6] Bump, Daniel, The Rankin-Selberg method: an introduction and survey, Ohio State Univ. Math. Res. Inst. Publ., 11. de Gruyter, Berlin, 2005, pp. 41-73.Google Scholar
[7] Casselman, William, Introduction to the theory of admissible representations of p-adic reductive groups. Séminaire Paul Sally, 1995. www.math.ubc.ca/∼cass/research/publications.htmlGoogle Scholar
[8] Digne, François and Michel, Jean, Groupes réductifs non connexes. Ann. Sci. École Norm. Sup. (4)27 (1994), no. 3, 345–406. http://dx.doi.Org/10.24033/asens.1696Google Scholar
[9] Feigon, Brooke, Lapid, Erez, and Offen, Omer, On representations distinguished by unitary groups. Publ. Math. Inst. Hautes Études Sci. 115 (2012), 185–323. http://dx.doi.Org/10.1007/s10240-012-0040-zGoogle Scholar
[10] Flicker, Yuval Z., On distinguished representations. J. Reine Angew. Math. 418 (1991), 139–172.Google Scholar
[11] Gan, Wee Teck and Takeda, Shuichiro, On Shalika periods and a theorem of Jacquet-Martin. Amer. J. Math. 132 (2010), no. 2, 475–528. http://dx.doi.Org/10.1353/ajm.0.0109Google Scholar
[12] Gel'fand, I. M. and Kajdan, D. A., Representations of the group GL(«, K) where K is a local field. Halsted, New York, 1975, pp. 95–118.Google Scholar
[13] Gurevich, Maxim and Offen, Omer, A criterion for integrability of matrix coefficients with respect to a symmetric space. J. Funct. Anal. 270 (2016), no. 12, 4478–4512. http://dx.doi.Org/10.101 6/j.jfa.2O1 6.02.008Google Scholar
[14] Hakim, Jeffrey and Murnaghan, Fiona, Two types of distinguished supercuspidal representations. Int. Math. Res. Not. (2002), no. 35, 1857-1889.Google Scholar
[15] Helminck, Aloysius G., Algebraic groups with a commuting pair of involutions and semisimple symmetric spaces. Adv. in Math. 71 (1988), no. 1, 21–91. http://dx.doi.Org/10.1016/0001-8708(88)90066-7Google Scholar
[16] Helminck, Aloysius G., Tori invariant under an involutorial automorphism. II. Adv. Math. 131 (1997), no. 1, 1-92. http://dx.doi.Org/10.1006/aima.1997.1633Google Scholar
[17] Helminck, A. G. and Helminck, G. F., A class of parabolic k-subgroups associated with symmetric k-varieties. Trans. Amer. Math. Soc. 350 (1998), no. 11, 4669–4691. http://dx.doi.org/10.1090/S0002-9947-98-02029-7Google Scholar
[18] Helminck, A. G. and Wang, S. P., On rationality properties of involutions of reductive groups. Adv. Math. 99 (1993), no. 1, 26–96. http://dx.doi.org/10.1006/aima.1993.1019Google Scholar
[19] Henniart, Guy, Correspondance de Langlands et fonctions L des carrés extérieur et symétrique. Int. Math. Res. Not. IMRN (2010), no. 4, 633-673.Google Scholar
[20] Heumos, Michael J. and Rallis, Stephen, Symplectic-Whittaker models for G\n. Pacific J. Math. 146 (1990), no. 2, 247–279. http://dx.doi.Org/10.2140/pjm.1990.146.247Google Scholar
[21] Jacquet, H., Piatetski-Shapiro, I.I., and Shalika, J. A., Rankin-Selberg convolutions. Amer. J. Math. 105 (1983), no. 2, 367–464. http://dx.doi.org/10.2307/2374264Google Scholar
[22] Jacquet, Hervé and Rallis, Stephen, Uniqueness of linear periods, Compositio Math. 102 (1996), no. 1, 65–123.Google Scholar
[23] Jiang, Dihua, Nien, Chufeng, and Qin, Yujun, Local Shalika models and functoriality. Manuscripta Math. 127 (2008), no. 2, 187–217. http://dx.doi.org/10.1007/s00229-008-0200-0Google Scholar
[24] Kable, Anthony C., Asai L-functions and Jacquet's conjecture. Amer. J. Math. 126 (2004), no. 4, 789–820. http://dx.doi.org/10.1353/ajm.2004.0030Google Scholar
[25] Kato, Shin-Ichi and Takano, Keiji, Subrepresentation theorem for p-adic symmetric spaces. Int. Math. Res. Not. IMRN (2008), no. 11.Google Scholar
[26] Kato, Shin-Ichi and Takano, Keiji, Square integrability of representations on p-adic symmetric spaces. J. Funct. Anal. 258 (2010), no. 5, 1427–1451. http://dx.doi.Org/10.1016/j.jfa.2009.10.026Google Scholar
[27] Kewat, Pramod Kumar and Raghunathan, Ravi, On the local and global exterior square L-functions of GLn . Math. Res. Lett. 19 (2012), no. 4, 785–804. http://dx.doi.org/10.4310/MRL.2012.v19.n4.a5Google Scholar
[28] Lagier, Nathalie, Terme constant de fonctions sur un espace symétrique réductif p-adique. J. Funct. Anal. 254 (2008), no. 4, 1088–1145. http://dx.doi.Org/10.1016/j.jfa.2007.07.012Google Scholar
[29] Lapid, Erez M. and Rogawski, Jonathan D., Periods of Eisenstein series: the Galois case. Duke Math. J. 120 (2003), no. 1, 153–226. http://dx.doi.org/10.1215/S0012-7094-03-12016-5Google Scholar
[30] Matringe, Nadir, Conjectures about distinction and local Asai L-functions. Int. Math. Res. Not. IMRN (2009), no. 9, 1699-1741.Google Scholar
[31] Matringe, Nadir, Linear and Shalika local periods for the mirabolic group, and some consequences. J. Number Theory 138 (2014), 1–19. http://dx.doi.Org/10.1016/j.jnt.2O13.11.012Google Scholar
[32] Murnaghan, Fiona, Regularity and distinction of supercuspidal representations. Contemp. Math., 543. Amer. Math. Soc, Providence, RI, 2011, pp. 155-183.Google Scholar
[33] Murnaghan, Fiona, Distinguished positive regular representations. To appear in Bull. Iran. Math. Soc.Google Scholar
[34] Offen, Omer and Sayag, Eitan, On unitary representations of GL2n distinguished by the symplectic group. J. Number Theory 125 (2007), no. 2, 344–355. http://dx.doi.Org/10.1016/j.jnt.2006.10.01 8Google Scholar
[35] Prasad, Dipendra, Invariant forms for representations of GL2 over a local field. Amer. J. Math. 114 (1992), no. 6, 1317–1363. http://dx.doi.org/10.2307/2374764Google Scholar
[36] Prasad, Dipendra, On the decomposition of a representation of GL(3) restricted to GL(2) over a p-adic field. Duke Math. J. 69 (1993), no. 1, 167–177. http://dx.doi.org/10.1215/S0012-7094-93-06908-6Google Scholar
[37] Prasad, Dipendra, A ‘relative’ local Langlands correspondence. arxiv:1512.04347Google Scholar
[38] Robert, Alain, Introduction to the representation theory of compact and locally compact groups. London Mathematical Society Lecture Note Series, 80. Cambridge University Press, Cambridge, 1983.Google Scholar
[39] Sakellaridis, Yiannis and Venkatesh, Akshay, Periods and harmonic analysis on spherical varieties. Astérisque 396 (2017), viii + 360.Google Scholar
[40] Shahidi, Freydoon, Twisted endoscopy and reducibility of induced representations for p-adic groups. Duke Math. J. 66 (1992), no. 1, 1–41. http://dx.doi.org/10.1215/S0012-7094-92-06601-4Google Scholar
[41] Smith, Jerrod Manford, Construction of relative discrete series representations for p-adic GLb . Ph.d. thesis, University of Toronto, June 2017.Google Scholar
[42] Zelevinsky, A. V., Induced representations of reductive p-adic groups. II. On irreducible representations of GL(n). Ann. Sci. École Norm. Sup. (4) 13 (1980), no. 2, 165–210. http://dx.doi.Org/10.24033/asens.1379Google Scholar