Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-18T12:47:25.331Z Has data issue: false hasContentIssue false
  • English
  • Français

Relative Darboux Theorem for Singular Manifolds and Local Contact Algebra

Published online by Cambridge University Press:  20 November 2018

M. Zhitomirskii
M. Zhitomirskii*
Affiliation:
Department of Mathematics, Technion, 32000 Haifa, Israel, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In 1999 V. Arnol’d introduced the local contact algebra: studying the problem of classification of singular curves in a contact space, he showed the existence of the ghost of the contact structure (invariants which are not related to the induced structure on the curve). Our main result implies that the only reason for existence of the local contact algebra and the ghost is the difference between the geometric and (defined in this paper) algebraic restriction of a 1-form to a singular submanifold. We prove that a germ of any subset 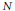$N$ of a contact manifold is well defined, up to contactomorphisms, by the algebraic restriction to 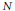$N$ of the contact structure. This is a generalization of the Darboux-Givental’ theorem for smooth submanifolds of a contact manifold. Studying the difference between the geometric and the algebraic restrictions gives a powerful tool for classification of stratified submanifolds of a contact manifold. This is illustrated by complete solution of three classification problems, including a simple explanation of V. Arnold's results and further classification results for singular curves in a contact space. We also prove several results on the external geometry of a singular submanifold 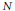$N$ in terms of the algebraic restriction of the contact structure to 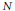$N$. In particular, the algebraic restriction is zero if and only if 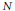$N$ is contained in a smooth Legendrian submanifold of 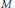$M$.

Keywords

Primary: 53D10secondary: 14B0558K50contact manifoldlocal contact algebrarelative Darboux theoremintegral curves
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 57 , Issue 6 , 01 December 2005 , pp. 1314 - 1340
Copyright
Copyright © Canadian Mathematical Society 2005

References

[Ar-1] Arnol’d, V. I., First steps of local contact algebra. Canad. J. Math. (6) 51(1999), 1123–1134.Google Scholar
[Ar-2] Arnol’d, V. I., First steps in local symplectic algebra. In: Differential Topology, Infinite-Dimensional Lie Algebras, and Applications. Fuchs’, D. B. 60th Anniversary Collection, (eds., Astashkevich, A. and Tabachnikov, S.), Amer. Math. Soc. Transl. Ser. 2, 194, American Mathematical Society, Providence, Rhode Island, 1999, pp. 1–8.Google Scholar
[Ar-3] Arnol’d, V. I., Simple singularities of curves. Proc. Steklov Inst.Math. 226(1999), 20–28.Google Scholar
[Ar-Gi] Arnol’d, V. I. and Givental, A. B., Symplectic geometry. Encyclopedia of Mathematical Sciences 4, Springer-Verlag, Berlin, Heidelberg, New York, 1990.Google Scholar
[Ar-Va-Gu] Arnol’d, V. I., Varchenko, A. M. and Gusein-Zade, S. M., Singularities of differentiable maps, vol. 1. Birkhauzer, Bazel, 1985.Google Scholar
[Do] Domitrz, W., private communication.Google Scholar
[Do-Ja-Zh-1] Domitrz, W., Janeczko, S. and Zhitomirskii, M., Relative Poincaré lemma, contractibility, quasi-homogeneity and vector fields tangent to a singular variety. To appear, Illinois J. Math. 48(2005).Google Scholar
[Do-Ja-Zh-2] Domitrz, W., Janeczko, S. and Zhitomirskii, M., Relative Darboux theorem for singular submanifolds of a symplectic manifold. In preparation.Google Scholar
[Gi] Givental’, A. B., Singular Lagrangian manifolds and their Lagrangian maps. J. Soviet Math. 52(1990), 3246–3278.Google Scholar
[Gi-Ho] Gibson, C. G. and Hobbs, C. A., Simple singularities of space curves. Math. Proc. Cambridge Philos. Soc. 113(1993), 297–310.Google Scholar
[Is] Ishikawa, G., Classifying singular Legendre curves by contactomorphisms. J. Geom. Phys. 52(2004), 113–126.Google Scholar
[Is-Ja] Ishikawa, G. and Janeczko, S., Symplectic bifurcations of plane curves and isotropic liftings. Quart. J. Math. 54(2003), 73–102.Google Scholar
[Zh-1] Zhitomirskii, M., Relative Darboux theorem for singular manifolds and singular curves in a contact space. Université de Bourgogne, Laboratoire de topologie, preprint 251.Google Scholar
[Zh-2] Zhitomirskii, M., Germs of integral curves in contact 3-space, plane and space curves. Isaac Newton Institute forMathematical Sciences, preprint NI00043-SGT, December, 2000.Google Scholar