Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Herrlich, Horst
1974.
Topological functors.
General Topology and its Applications,
Vol. 4,
Issue. 2,
p.
125.
Banaschewski, Bernhard
and
Nelson, Evelyn
1976.
Tensor Products and Bimorphisms.
Canadian Mathematical Bulletin,
Vol. 19,
Issue. 4,
p.
385.
Porst, Hans -E.
1977.
On underlying functors in general and topological algebra.
Manuscripta Mathematica,
Vol. 20,
Issue. 3,
p.
209.
Tholen, Walter
1977.
FACTORIZATIONS OF CONES ALONG A FUNCTOR.
Quaestiones Mathematicae,
Vol. 2,
Issue. 1-3,
p.
335.
Fay, Temple H.
1977.
AN AXIOMATIC APPROACH TO CATEGORIES OF TOPOLOGICAL ALGEBRAS.
Quaestiones Mathematicae,
Vol. 2,
Issue. 1-3,
p.
113.
Tholen, Walter
1978.
On Wyler's Taut lift theorem.
General Topology and its Applications,
Vol. 8,
Issue. 2,
p.
197.
Tholen, Walter
1978.
Zum Satz von Freyd und Kelly.
Mathematische Annalen,
Vol. 232,
Issue. 1,
p.
1.
Nakagawa, Ryosuke
1979.
Categorical Topology.
Vol. 719,
Issue. ,
p.
250.
Tholen, Walter
1979.
Categorical Topology.
Vol. 719,
Issue. ,
p.
376.
Porst, Hans-E.
and
Wischnewsky, Manfred B.
1979.
Categorical Topology.
Vol. 719,
Issue. ,
p.
277.
Hoffmann, Rudolf-E.
1979.
Factorization of Cones.
Mathematische Nachrichten,
Vol. 87,
Issue. 1,
p.
221.
Herrlich, H.
and
Strecker, G. E.
1979.
Categorical Topology.
Vol. 719,
Issue. ,
p.
150.
Tholen, Walter
1979.
Semi-topological functors I.
Journal of Pure and Applied Algebra,
Vol. 15,
Issue. 1,
p.
53.
Nel, L. D.
1979.
Categorical Topology.
Vol. 719,
Issue. ,
p.
259.
Meseguer, José
1980.
Varieties of chain-complete algebras.
Journal of Pure and Applied Algebra,
Vol. 19,
Issue. ,
p.
347.
Pumpl�n, Dieter
1980.
Initial morphisms and monomorphisms.
Manuscripta Mathematica,
Vol. 32,
Issue. 3-4,
p.
309.
Street, Ross
Tholen, Walter
Wischnewsky, Manfred
and
Wolff, Harvey
1980.
Semi-topological functors III: Lifting of monads and adjoint functors.
Journal of Pure and Applied Algebra,
Vol. 16,
Issue. 3,
p.
299.
Nel, L.D.
1981.
Universal topological algebra needs closed topological categories.
Topology and its Applications,
Vol. 12,
Issue. 3,
p.
321.
Nel, L. D.
1982.
Categorical Aspects of Topology and Analysis.
Vol. 915,
Issue. ,
p.
247.
Min, Kyung Chan
1983.
EXPONENTIAL LAWS FOR ORDERED “TOPOLOGICAL” VECTOR SPACES.
Quaestiones Mathematicae,
Vol. 6,
Issue. 1-3,
p.
177.


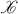 be a category with nice factorization-properties. If a functor
be a category with nice factorization-properties. If a functor 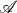 —>
—> 