Article contents
Reducibility of the Principal Series for 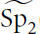 (F) over a p-adic Field
(F) over a p-adic Field
Published online by Cambridge University Press: 20 November 2018
Abstract
Let 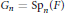 ${{G}_{n}}=\text{S}{{\text{p}}_{n}}\left( F \right)$ be the rank
${{G}_{n}}=\text{S}{{\text{p}}_{n}}\left( F \right)$ be the rank 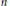 $n$ symplectic group with entries in a nondyadic
$n$ symplectic group with entries in a nondyadic 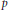 $p$-adic field
$p$-adic field  $F$. We further let
$F$. We further let
 ${{\tilde{G}}_{n}}$
be the metaplectic extension of
${{\tilde{G}}_{n}}$
be the metaplectic extension of 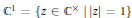 ${{G}_{n}}\,\text{by}\,{{\mathbb{C}}^{1}}=\left\{ z\in {{\mathbb{C}}^{\times }}|\,|z|=1 \right\}$ defined using the Leray cocycle. In this paper, we aim to demonstrate the complete list of reducibility points of the genuine principal series of
${{G}_{n}}\,\text{by}\,{{\mathbb{C}}^{1}}=\left\{ z\in {{\mathbb{C}}^{\times }}|\,|z|=1 \right\}$ defined using the Leray cocycle. In this paper, we aim to demonstrate the complete list of reducibility points of the genuine principal series of 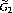 ${{\tilde{G}}_{2}}$. In most cases, we will use some techniques developed by Tadić that analyze the Jacquet modules with respect to all of the parabolics containing a fixed Borel. The exceptional cases involve representations induced from unitary characters
${{\tilde{G}}_{2}}$. In most cases, we will use some techniques developed by Tadić that analyze the Jacquet modules with respect to all of the parabolics containing a fixed Borel. The exceptional cases involve representations induced from unitary characters 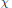 $\chi $ with
$\chi $ with  ${{\chi }^{2}}=1$. Because such representations
${{\chi }^{2}}=1$. Because such representations  $\pi $ are unitary, to show the irreducibility of
$\pi $ are unitary, to show the irreducibility of  $\pi $, it suffices to show that
$\pi $, it suffices to show that
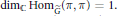 ${{\dim}_{\mathbb{C}}}\,\text{Ho}{{\text{m}}_{{\tilde{G}}}}\left( \pi ,\,\pi \right)\,=\,1$
. We will accomplish this by examining the poles of certain intertwining operators associated to simple roots. Then some results of Shahidi and Ban decompose arbitrary intertwining operators into a composition of operators corresponding to the simple roots of
${{\dim}_{\mathbb{C}}}\,\text{Ho}{{\text{m}}_{{\tilde{G}}}}\left( \pi ,\,\pi \right)\,=\,1$
. We will accomplish this by examining the poles of certain intertwining operators associated to simple roots. Then some results of Shahidi and Ban decompose arbitrary intertwining operators into a composition of operators corresponding to the simple roots of
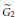 ${{\tilde{G}}_{2}}.$ We will then be able to show that all such operators have poles at principal series representations induced from quadratic characters and therefore such operators do not extend to operators in
${{\tilde{G}}_{2}}.$ We will then be able to show that all such operators have poles at principal series representations induced from quadratic characters and therefore such operators do not extend to operators in
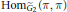 $\text{Ho}{{\text{m}}_{{{{\tilde{G}}}_{2}}}}\left( \pi ,\,\pi \right)$
for the
$\text{Ho}{{\text{m}}_{{{{\tilde{G}}}_{2}}}}\left( \pi ,\,\pi \right)$
for the  $\pi $ in question.
$\pi $ in question.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2010
References
- 4
- Cited by


