Article contents
Reducibility in Aℝ(K), Cℝ(K), and A(K)
Published online by Cambridge University Press: 20 November 2018
Abstract
Let 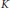 $K$ denote a compact real symmetric subset of
$K$ denote a compact real symmetric subset of  $\mathbb{C}$ and let
$\mathbb{C}$ and let 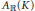 ${{A}_{\mathbb{R}}}\left( K \right)$ denote the real Banach algebra of all real symmetric continuous functions on
${{A}_{\mathbb{R}}}\left( K \right)$ denote the real Banach algebra of all real symmetric continuous functions on 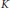 $K$ that are analytic in the interior
$K$ that are analytic in the interior 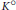 ${{K}^{\circ }}$ of
${{K}^{\circ }}$ of 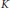 $K$, endowed with the supremum norm. We characterize all unimodular pairs
$K$, endowed with the supremum norm. We characterize all unimodular pairs 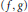 $\left( f,\,g \right)$ in
$\left( f,\,g \right)$ in 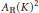 ${{A}_{\mathbb{R}}}{{\left( K \right)}^{2}}$ which are reducible. In addition, for an arbitrary compact
${{A}_{\mathbb{R}}}{{\left( K \right)}^{2}}$ which are reducible. In addition, for an arbitrary compact 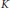 $K$ in
$K$ in  $\mathbb{C}$, we give a new proof (not relying on Banach algebra theory or elementary stable rank techniques) of the fact that the Bass stable rank of
$\mathbb{C}$, we give a new proof (not relying on Banach algebra theory or elementary stable rank techniques) of the fact that the Bass stable rank of 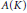 $A\left( K \right)$ is 1. Finally, we also characterize all compact real symmetric sets
$A\left( K \right)$ is 1. Finally, we also characterize all compact real symmetric sets 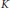 $K$ such that
$K$ such that 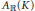 ${{A}_{\mathbb{R}}}\left( K \right)$, respectively
${{A}_{\mathbb{R}}}\left( K \right)$, respectively 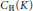 ${{C}_{\mathbb{R}}}\left( K \right)$, has Bass stable rank 1.
${{C}_{\mathbb{R}}}\left( K \right)$, has Bass stable rank 1.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2010
References
- 4
- Cited by


