Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-18T20:55:53.331Z Has data issue: false hasContentIssue false
  • English
  • Français

Rational Models of the Complement of a Subpolyhedron in a Manifold with Boundary

Published online by Cambridge University Press:  20 November 2018

Hector Cordova Bulens ,
Pascal Lambrechts  and
Don Stanley
Hector Cordova Bulens
Affiliation:
IRMP, Université catholique de Louvain, 2 Chemin du Cyclotron, B-1348 Louvain-la-Neuve, Belgium e-mail: [email protected]@uclouvain.be
Pascal Lambrechts
Affiliation:
IRMP, Université catholique de Louvain, 2 Chemin du Cyclotron, B-1348 Louvain-la-Neuve, Belgium e-mail: [email protected]@uclouvain.be
Don Stanley
Affiliation:
University of Regina, Department of Mathematics and Statistics, College West, Regina e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 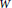$W$ be a compact simply connected triangulated manifold with boundary and let 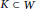$K\,\subset \,W$ be a subpolyhedron. We construct an algebraic model of the rational homotopy type of 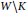$W\text{ }\!\!\backslash\!\!\text{ K}$ out of a model of the map of pairs 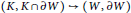$\left( K,\,K\cap \partial W \right)\,\to \,\left( W,\,\partial W \right)$ under some high codimension hypothesis.

We deduce the rational homotopy invariance of the configuration space of two points in a compact manifold with boundary under 2-connectedness hypotheses. Also, we exhibit nice explicit models of these configuration spaces for a large class of compact manifolds.

Keywords

55P6255R80Lefschetz dualitySullivan modelconfiguration space
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 70 , Issue 2 , 01 April 2018 , pp. 265 - 293
Copyright
Copyright © Canadian Mathematical Society 2018

References

[1] Cohen, F. R. and Taylor, L. R., Configuration spaces: applications to Gelfand-Fuks cohomology. Bull. Amer. Math. Soc. 84(1978), no. 1, 134–136.http://dx.doi.org/10.1090/S0002-9904-1978-14440-1 Google Scholar
[2] Cordova Bulens, H., Rational model of the configuration space of two points in a simply connected closed manifold. Proc. Amer. Math. Soc. 143(2015), no. 12, 5437–5453.http://dx.doi.Org/10.1090/proc/12666 Google Scholar
[3] Cordova Bulens, H., Lambrechts, P., and Stanley, D., Pretty rational models for Poincaré duality pairs. http://arxiv:1505.04818 Google Scholar
[4] Curtis, E. B., Simplicial homotopy theory. Advances in Math. 6(1971), 107–209.http://dx.doi.Org/10.1016/0001-8708(71)90015-6 Google Scholar
[5] Félix, Y., Halperin, S., and Thomas, J.-C., Rational homotopy theory. Graduate Texts in Mathematics , 205, Springer-Verlag, New York, 2001.http://dx.doi.Org/10.1007/978-1-4613-0105-9 Google Scholar
[6] Hudson, J. F. P., Piecewise linear topology. University of Chicago Lecture Notes prepared with the assistance of J. L. Shaneson and J. Lees , W. A. Benjamin, Inc., New York-Amsterdam, 1969.Google Scholar
[7] Lambrechts, P. and Stanley, D., The rational homotopy type of configuration spaces of two points. Ann. Inst. Fourier (Grenoble) 54(2004), no. 4, 1029–1052.http://dx.doi.Org/10.58O2/aif.2O42 Google Scholar
[8] Lambrechts, P. and Stanley, D., Algebraic models of Poincaré embeddings. Algebr. Geom. Topol. 5(2005), 135–182.http://dx.doi.Org/10.2140/agt.2005.5.135 Google Scholar
[9] Lambrechts, P. and Stanley, D., Poincaré duality and commutative differential graded algebras. Ann. Sci. ác. Norm. Super. (4) 41(2008), no. 4, 495–509.Google Scholar
[10] Lambrechts, P. and Stanley, D., A remarkable DGmodule model for configuration spaces. Algebr. Geom. Topol. 8(2008), no. 2, 1191–1222.http://dx.doi.Org/10.2140/agt.2008.8.1191 Google Scholar
[11] Longoni, R. and Salvatore, P., Configuration spaces are not homotopy invariant. Topology 44(2005), no. 2, 375–380. http://dx.doi.Org/10.1016/j.top.2004.11.002 Google Scholar
[12] Weibel, C. A., An introduction to homological algebra. Cambridge Studies in Advanced Mathematics , 38, Cambridge University Press, Cambridge, 1994.http://dx.doi.org/10.1017/CBO9781139644136 Google Scholar