Published online by Cambridge University Press: 20 November 2018
Let 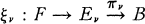 be two Serre fibrations with same base and fibre in which all the spaces have the homotopy type of simple CW complexes of finite type. We say they are rationally homotopically equivalent if there is a homotopy equivalence
be two Serre fibrations with same base and fibre in which all the spaces have the homotopy type of simple CW complexes of finite type. We say they are rationally homotopically equivalent if there is a homotopy equivalence 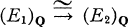 between the localizations at Q which covers the identity map of BQ.
between the localizations at Q which covers the identity map of BQ.
Such an equivalence implies, of course, an isomorphism of cohomology algebras (over Q) and of rational homotopy groups; on the other hand isomorphisms of these classical algebraic invariants are usually (by far) insufficient to establish the existence of a rational homotopy equivalence.
Nonetheless, as we shall show in this note, for certain fibrations rational homotopy equivalence is in fact implied by the existence of an isomorphism of cohomology algebras. While these fibrations are rare inside the class of all fibrations, they do include principal bundles with structure groups a connected Lie group G as well as many associated bundles with fibre G/K.