Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-30T22:35:07.208Z Has data issue: false hasContentIssue false
  • English
  • Français

Ranks of Algebras of Continuous C*-Algebra Valued Functions

Published online by Cambridge University Press:  20 November 2018

Masaru Nagisa ,
Hiroyuki Osaka  and
N. Christopher Phillips
Masaru Nagisa
Affiliation:
Department of Mathematics and Informatics, Chiba University, Yayoi-cho 1-33, Inage-ku, Chiba City 263-8522, Japan
Hiroyuki Osaka
Affiliation:
Department of Mathematical Sciences, Ritsumeikan University, Kusatsu, Shiga, 525-8577, Japan
N. Christopher Phillips
Affiliation:
Department of Mathematics, University of Oregon, Eugene, Oregon 97403-1222, USA
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove a number of results about the stable and particularly the real ranks of tensor products of 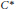${{C}^{*}}$ -algebras under the assumption that one of the factors is commutative. In particular, we prove the following:

  1. (1) If 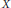$X$ is any locally compact $\sigma $-compact Hausdorff space and 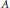$A$ is any 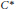${{C}^{*}}$-algebra, then 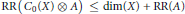$\text{RR(}{{C}_{0}}\text{(}X\text{)}\otimes A\text{)}\le \text{dim(}X\text{)+RR(}A\text{)}$ .

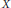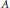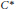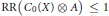  2. (2) If $X$ is any locally compact Hausdorff space and $A$ is any purely infinite simple ${{C}^{*}}$ -algebra, then $\text{RR(}{{C}_{0}}\text{(}X\text{)}\otimes A\text{)}\le 1$ .

  3. (3) 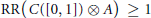$\text{RR(}C([0,\,1]\,)\otimes \,A)\,\ge \,1$ for any nonzero 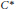${{C}^{*}}$-algebra 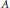$A$, and 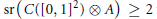$\text{sr(}C({{[0,\,1]}^{2}})\,\otimes \,A\text{)}\,\ge \,2$ for any unital 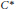${{C}^{*}}$-algebra 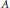$A$.

  4. (4) If 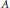$A$ is a unital 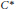${{C}^{*}}$-algebra such that 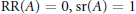$\text{RR(}A\text{)}\,\text{=}\,\text{0,}\,\text{s}r\text{(}A\text{)}\,\text{=}\,\text{1}$, and 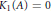${{K}_{1}}(A)=0$ , then 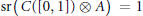$\text{sr(}C([0,\,1])\,\otimes \,A\text{)}\,\text{=}\,1$.

  5. (5) There is a simple separable unital nuclear 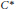${{C}^{*}}$-algebra 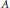$A$ such that 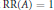$\text{RR(}A\text{)}\,\text{=}\,\text{1}$ and 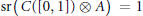$\text{sr(}C([0,\,1])\,\otimes \,A\text{)}\,\text{=}\,1$.

Keywords

46L0546L5246L8019A1319B10
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 53 , Issue 5 , 01 October 2001 , pp. 979 - 1030
Copyright
Copyright © Canadian Mathematical Society 2001

References

[1] Akemann, C. A. and Pedersen, G. K., Ideal perturbations of elements in C*-algebras. Math. Scand. 41(1977), 117–139.Google Scholar
[2] Akemann, C. A. and Shultz, F., Perfect C*-algebras. Memoirs Amer. Math. Soc. 326, 1985.Google Scholar
[3] Arveson, W., Notes on extensions of C*-algebras. Duke Math. J. 44(1977), 329–355.Google Scholar
[4] Beggs, E. J. and Evans, D. E., The real rank of algebras of matrix valued functions. Internat. J. Math. 2(1991), 131–137.Google Scholar
[5] Brown, L. G. andPedersen, G. K., C*-algebras of real rank zero. J. Funct. Anal. 99(1991), 131–149.Google Scholar
[6] Cuntz, J., K-Theory for certain C*-algebras. Ann. of Math. 113(1981), 181–197.Google Scholar
[7] Dădărlat, M., Nonnuclear subalgebras of AF algebras. Amer. J. Math. 122(2000), 581–597.Google Scholar
[8] Dădărlat, M., Nagy, G., Némethi, A., and Pasnicu, C., Reduction of topological stable rank in inductive limit of C*-algebras. Pacific J. Math. 153(1992), 267–276.Google Scholar
[9] Eilenberg, S. and Steenrod, N. E., Foundations of Algebraic Topology. Princeton University Press, Princeton, 1952.Google Scholar
[10] Hassan, N. Elhage, Rangs stables de certaines extensions. J. LondonMath. Soc. (2) 52(1993), 605–624.Google Scholar
[11] Hassan, N. Elhage, Rang réel de certaines extensions. Proc. Amer. Math. Soc. 123(1995), 3067–3073.Google Scholar
[12] Elliott, G. A., Gong, G., and Li, L., On the classification of simple inductive limit C*-algebras, II: The isomorphism theorem. Preprint.Google Scholar
[13] Goodearl, K. R., Notes on a class of simple C*-algebras with real rank zero. Publ. Mat. (Barcelona) 36(1992), 637–654.Google Scholar
[14] Herman, R. H. and Vaserstein, L. N., The stable range of C*-algebras. Invent. Math. 77(1984), 553–555.Google Scholar
[15] Kadison, R. V. and Ringrose, J. R., Fundamentals of the Theory of Operator Algebras, Volume II. Academic Press, New York-London-Paris-San Diego-San Francisco-São Paulo-Sydney-Tokyo- Toronto, 1983.Google Scholar
[16] Kodaka, K. and Osaka, H., FS-property for C*-algebras. Proc. Amer.Math. Soc. 129(2001), 999–1003.Google Scholar
[17] Lin, H., Generalized Weyl-von Neumann Theorem (II). Math. Scand. 77(1995), 129–147.Google Scholar
[18] Lin, H. and Phillips, N. C., Classification of direct limits of even Cuntz-circle algebras. Mem. Amer. Math. Soc. 565, 1995.Google Scholar
[19] Loring, T. A., C*-algebras generated by stable relations. J. Funct. Anal. 112(1993), 159–203.Google Scholar
[20] Lundell, A. T. and Weingram, S., The Topology of CW Complexes. Van Nostrand Reinhold Company, New York-Cincinnati-Toronto-London-Melbourne, 1969.Google Scholar
[21] Mardešič, S. and Rubin, L. R., Approximate inverse systems of compacta and covering dimension. Pacific J. Math. 138(1989), 129–144.Google Scholar
[22] Murphy, G. J. and Phillips, N. C., C*-algebras with the approximate positive factorization property. Trans. Amer. Math. Soc. 348(1996), 2291–2306.Google Scholar
[23] Osaka, H., Real rank of crossed products by connected compact groups. Bull. London Math. Soc. 27(1995), 257–264.Google Scholar
[24] Osaka, H., Certain C*-algebras with non-zero real rank and extremal richness. Math. Scand. 85(1999), 79–86.Google Scholar
[25] Pears, A. R., Dimension Theory of General Spaces. Cambridge University Press, Cambridge-London-New York-Melbourne, 1975.Google Scholar
[26] Phillips, N. C., Reduction of exponential rank in direct limits of C*-algebras. Canadian J. Math. 46(1994), 818–853.Google Scholar
[27] Phillips, N. C., A classification theorem for nuclear purely infinite simple C*-algebras. Doc. Math. 5(2000), 49–114 (electronic).Google Scholar
[28] Phillips, N. C., Real and exponential rank of tensor products with . J. Operator Theory, to appear.Google Scholar
[29] Phillips, N. C., Many nonisomorphic nonnuclear simple C*-algebras with the same Elliott invariant. In preparation.Google Scholar
[30] Pontrjagin, L. S., Sur une hypothèse fondamentale de la théorie de la dimension. C. R. Acad. Sci. Paris Sér. A–B 190(1930), 1105–1107.Google Scholar
[31] Rieffel, M. A., Dimension and stable rank in the K-theory of C*-algebras. Proc. LondonMath. Soc. 46(1983), 301–333.Google Scholar
[32] Rieffel, M. A., The homotopy groups of the unitary groups of non-commutative tori. J. Operator Theory 17(1987), 237–254.Google Scholar
[33] Zhang, S., A property of purely infinite simple C*-algebras. Proc. Amer. Math. Soc. 109(1990), 717–720.Google Scholar
[34] Zhang, S., Certain C*-algebras with real rank zero and their corona and multiplier algebras, Part 1. Pacific J. Math. 155(1992), 169–197.Google Scholar
[35] Zhang, S., On the homotopy type of the unitary group and the Grassmann space of purely infinite simple C*-algebras. K-Theory, to appear.Google Scholar